Difference between revisions of "Range Search"
m (spelling and grammar corrections, I was unsure what you meant in some places. I did my best to change these, but you should make sure I didn't remove anything you wanted to keep.) |
m (link to R-Tree implementation added) |
||
| (5 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | '''Range search''' is a data analysis algorithm, which is very similar to [[Dynamic Clustering|k-NN]]. The main difference is that k-NN gets a fixed number of data points while range search does not. | + | '''Range search''' is a data analysis algorithm, which is very similar to [[Dynamic Clustering|k-NN]] algorithm. The main difference is that k-NN gets a fixed number of data points while range search does not. |
== How it works == | == How it works == | ||
Record state (aka situation, turn snapshot, etc.) with some set of attributes (velocity, acceleration, x, y, etc.). When you need data, calculate some hypercube centered at the current situation. For example, if the current situation is {velocity = 8, acceleration = 0, x = 200, y = 200}, then hypercube can be described as the set of intervals {[6,8], [0,0], [180, 220], [180, 220]}. Then iterate through all data and select the points that are contained by this hypercube. Then use these data points for targeting, movement, etc. | Record state (aka situation, turn snapshot, etc.) with some set of attributes (velocity, acceleration, x, y, etc.). When you need data, calculate some hypercube centered at the current situation. For example, if the current situation is {velocity = 8, acceleration = 0, x = 200, y = 200}, then hypercube can be described as the set of intervals {[6,8], [0,0], [180, 220], [180, 220]}. Then iterate through all data and select the points that are contained by this hypercube. Then use these data points for targeting, movement, etc. | ||
| − | == Advantages == | + | == Advantages & Disadvantages == |
| − | The main advantage of range | + | The main advantage of range searching over the k-NN algorithm is that range searching gets only corresponding data. The k-NN algorithm can get data points that do not correspond to the current situation if ''k'' is too high for the current data, or it may ignore relevant data, if ''k'' is much less than the number of data points 'around' the current situation. |
| + | |||
| + | But at the same time, with lesser data (i.e. at the beginning of the match), k-NN algorithm can utilize all data available automatically, while range searching, like visit count stats, may get limited or no data at all. This does not apply in multiple buffers system. | ||
== Illustrations == | == Illustrations == | ||
Legend: | Legend: | ||
| − | * little black dots - data points | + | * little black dots ({{dot}}) - data points |
| − | * big red dots - current situation | + | * big red dots (<span style="color:red;font-size:200%;line-height:50%">{{dot}}</span>) - current situation |
* red areas - area of data points used for data analysis | * red areas - area of data points used for data analysis | ||
{| border="1" cellspacing="0" cellpadding="5" | {| border="1" cellspacing="0" cellpadding="5" | ||
| [[File:Knn.gif|K nearest neighbours algorithm]] || [[File:Rs.gif|Range search algorithm]] || [[File:Vcs.gif|Visit count stats algorithm]] | | [[File:Knn.gif|K nearest neighbours algorithm]] || [[File:Rs.gif|Range search algorithm]] || [[File:Vcs.gif|Visit count stats algorithm]] | ||
|- | |- | ||
| − | |align="center"| [[Dynamic Clustering|k-nearest neighbours]] algorithm ||align="center"| '''Range search''' algorithm ||align="center"| [[Visit Count Stats]] algorithm | + | |align="center"| [[Dynamic Clustering|k-nearest neighbours]] algorithm<br/>with Euclidian distance formula ||align="center"| '''Range search''' algorithm ||align="center"| [[Visit Count Stats]] algorithm |
|} | |} | ||
| Line 21: | Line 23: | ||
* [[Dynamic Clustering]] (k-nearest neighbors) | * [[Dynamic Clustering]] (k-nearest neighbors) | ||
* [[Visit Count Stats]] | * [[Visit Count Stats]] | ||
| + | * [[User:Jdev/Code/R_Tree|R-Tree implementation]] | ||
[[Category:Log-Based Algorithms]] | [[Category:Log-Based Algorithms]] | ||
Latest revision as of 11:57, 20 December 2011
Range search is a data analysis algorithm, which is very similar to k-NN algorithm. The main difference is that k-NN gets a fixed number of data points while range search does not.
How it works
Record state (aka situation, turn snapshot, etc.) with some set of attributes (velocity, acceleration, x, y, etc.). When you need data, calculate some hypercube centered at the current situation. For example, if the current situation is {velocity = 8, acceleration = 0, x = 200, y = 200}, then hypercube can be described as the set of intervals {[6,8], [0,0], [180, 220], [180, 220]}. Then iterate through all data and select the points that are contained by this hypercube. Then use these data points for targeting, movement, etc.
Advantages & Disadvantages
The main advantage of range searching over the k-NN algorithm is that range searching gets only corresponding data. The k-NN algorithm can get data points that do not correspond to the current situation if k is too high for the current data, or it may ignore relevant data, if k is much less than the number of data points 'around' the current situation.
But at the same time, with lesser data (i.e. at the beginning of the match), k-NN algorithm can utilize all data available automatically, while range searching, like visit count stats, may get limited or no data at all. This does not apply in multiple buffers system.
Illustrations
Legend:
- little black dots ( · ) - data points
- big red dots ( · ) - current situation
- red areas - area of data points used for data analysis
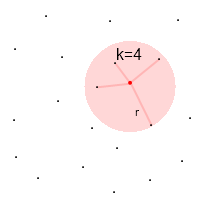 |
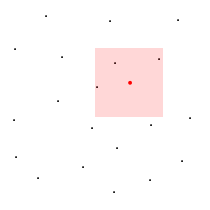 |
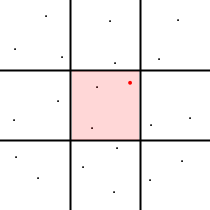
|
| k-nearest neighbours algorithm with Euclidian distance formula |
Range search algorithm | Visit Count Stats algorithm |
See also
- Dynamic Clustering (k-nearest neighbors)
- Visit Count Stats
- R-Tree implementation