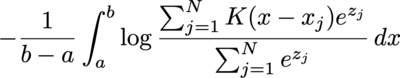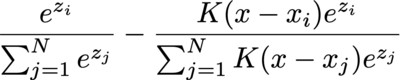Thread:Talk:BeepBoop/Understanding BeepBoop/Property of gradient of cross-entropy loss with kernel density estimation

I'm quite curious about the behavior of cross entropy loss between a uniform distribution and kernel density estimation with softmax weight:

where a and b is the lower and upper bound of the target uniform distribution, K is the kernel function (assume normalized), x_j is the angle of the data point, and z_j the weight before softmax.

The integral is often calculated by numerical methods, such as binning, so let's consider the gradient of the i-th data point's weight before softmax, and consider only one of the bins (with angle x) and ignore the values multiplied before integral:

It degenerates to ordinary cross entropy loss with softmax when K is either 1 or 0 (and 1 iif the "label" matches): S_i - 1 when label matches or S_i when label mismatches.

But things start to get interesting when K is different.

The scale of K(x - x_i) doesn't matter at all (e.g. when all data point is far from target distribution). The effective learning rate is same when two data points are equally near the target distribution, or when they are equally far from the target distribution.