Approximate ELO

I have been mulling around ways to approximate ELO for awhile. Since originally it was used for ranking (2000 club, etc), however the rankings have drifted considerably and with the advent of APS there is no real need for it. However the number is still nice, even if the methods for calculating it have problems.

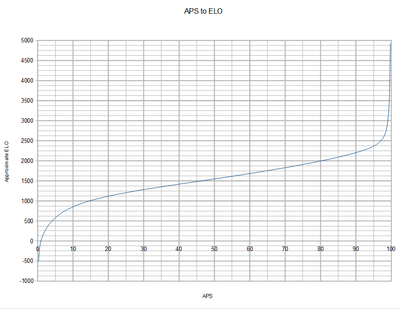
So I figured we could get our nice number without a lot of number crunching with way of a simple equation. At least that was the original theory. However APS doesn't map very well to ELO, which is not at all linear, and the data set required for calculating such an equation is incomplete.

However here are my token efforts at doing just that. The dataset I used was the 2009 Glinko-2 and APS, as it was likely the most similar to the old ELO rankings. I would ahve used those, but they lacked an APS column, and the common bots between them don't exactly line up very well (plus that decimates my data set even more).

public static final double calculateElo(double x) {
	double a = 169.1;
	double b = 0.02369;
	double c = 334.2;
	return a*Math.cosh(b*x)+c*Math.log(x);
}
public static final double calculateEloFast(double x) {
	double a = 0.7082e-03;
	double b = -0.3340e-05;
	double c = 0.3992e-02;
	return 1.0/(a+b*x+c/x);
}

The first is a bit more accurate. 0 is negative infinity, and 100 is around 2450 (it should be positive infinity, but I did what I could). However with a logarithm and a cosh, it is a bit heavy to be called 700+ times every a page loads (I think at least). The second is a slightly less accurate system, 0 is 0 and 100 is about 2415. With mostly simple math it is much easier to execute.

So thoughts, concerns, scorn?

For a precise ELO calculation you would need the full pairwise matrix. But for an approximation based on an APS column, it looks good.

Another way to deal with rating drift (without the full pairwise matrix) is calculating the average of all ELO ratings, then calculate the difference from the average to 1600, then add/subtract the difference to all drifted ratings. So you have ratings centered around 1600. Works with both ELO and Glicko-2 ratings columns.

Does it currently do that? The Glinko-2 has drifted up, the 2000 club now consists of only the top 16 bots.

Which is why I was considering trying to make a Approximate version. However, with mine instead of drifting down I think I see higher bots drifting up, and lower bots drifting even more down. I think this is because as new lower bots are added the APS for higher robots go up, and robots that did worse against it go down.

So it faces an entirely different kind of drift, but at least the center seems stable.

ELO/Glicko-2 work with differences between ratings.

The more competitors the ranking has, the more the rating difference between first and last places will be. This is normal.

But ELO has another drifting problem due to deflation. All competitors ratings going down because most retired competitors have ratings above the average.

static final double DRIFTED_ELO_AVERAGE = -2397.92418506835;

static final double DRIFTED_GLICKO2_AVERAGE = 1468.99474237645;

static final double DESIRED_AVERAGE = 1600;

static double calculateElo(double driftedElo) {
    return driftedElo - DRIFTED_ELO_AVERAGE + DESIRED_AVERAGE;
}

static double calculateGlicko2(double driftedGlicko2) {
    return driftedGlicko2 - DRIFTED_GLICKO2_AVERAGE + DESIRED_AVERAGE;
}

I'd be fine with a new ELO formula to replace the currently useless one, but I can't see myself ever again caring about ELO or Glicko over straight APS for the main overall score rating. APS is clear, stable, accurate and meaningful, and ELO/Glicko just seem like attempts to solve a problem we don't have. As far as new permanent scoring methods, I'm much more interested in the Condorcet / Schulze / APW ideas brought up in the discussions on Talk:Offline batch ELO rating system, Talk:King maker, and Talk:Darkcanuck/RRServer/Ratings#Schulze_.26_Tideman_Condorcet. I also really like what Skilgannon did with ANPP in LiteRumble, where 0 is the worst score against a bot and 100 is the best score against a bot, scaling linearly.

The main advantage of ELO/Glicko-2 over other systems is they work well with incomplete pairings, and yes, we almost don´t have problems related to incomplete pairings.

But there are other smaller advantages, like higher accuracy with scores near 0% or 100% due to its S shaped (logistic distribution) function. Being able to "forget" the past also makes ELO/Glicko-2 adequate in meleerumble where historical contamination is an issue.

And I would really like to see a Ranked Pairs ranking. This would bring something new to the rumble. It is superior to the current PL (Copeland) system in almost every way, except maybe CPU/memory performance. I was thinking in building another RoboRumble server myself, designed specifically to calculate complex rankings like Ranked Pairs. But didn´t find the time to do it yet.

The thing about ranked pairs is that I haven't seen any which provide absolute scores per bot, rather than relative scores - I guess this is just part of the definition? Because of this there isn't any way to make partial improvements however, which makes it meaningless as a testing metric. Also, they are usually difficult to understand (conceptually), so understanding which pairing is causing a score loss is harder. That's why I like the Win% and Vote% as metrics for robustness, and APS for overall strength, because they are easy to understand, calculate and identify problem bots.

In Ranked Pairs, competitors causing problems are always above in the ranking, with the one causing most problems almost always directly above. Competitors below in the ranking never cause problems.

Unless you are competing for the bottom, when you reverse the logic. Competitors causing problems are always below, and competitors above never cause problems.

Although the calculation is complex, the resulting ranking follows a rather straighforward transitive logic. Winners staying above losers, with this always being true between adjacent competitors in the ranking.

This is due to 3 criteria being met at the same time, ISDA, LIIA and cloneproof.

But Ranked Pairs is not meant to replace APS or ELO, it is meant to replace PL (Copeland). APS and ELO give a rating which helps track improvement while Ranked Pairs and Copeland don´t.

I think if you add a d/(100-x) term it will improve the fit near the top. Perhaps use d*(100-x)^e for the slow/accurate version, although you can't use simple linear algebra to find the best e then, a genetic approach would probably be better.

I like the idea of this, just for historical reasons to have a decent mapping of APS to ELO, and would consider adding a column in the LiteRumble page for it. I would calculate this on the fly as the page loads, since for me with Python on App Engine the slow part of the code is the interpretation of the code, not the individual math operations the code calls =)Of course I'd have to test to make sure it doesn't slow it down too much, but it should be fine, the fast version if nothing else.

Here are some graphs.

If you want to enforce a specific rating for a specific competitor, you can also adjust the DESIRED_AVERAGE in the algorithm above so ratings match what you want.

The real challenge is making multiple bots line up, which is about what I managed here.

If you change the rating difference between competitors, you distort expected score estimation, PBI and specialization indexes. It is no longer ELO-like.

That´s why the code I put above shifts all competitors up or down equally.

Looks pretty good. Any chance you could show that first graph overlayed with a scatter plot of the training samples you used?

The first one was generated (calcelofast). I used all samples from 2009 rumble archive aps and glinko-2.

From there it was hand tuned to be honest.

Wow, ok. It would only be a couple lines of Matlab/Scilab to do a proper regression though. Wouldn't that be better?

If you want to do one. You can just get the output from the algorithm and use those as the samples.

(I don't have MatLab actually).

Try this: elo(APS) = -300*ln(100/APS - 1) + 1600

It uses a reflected normal sigmoid so (I think) it's based off of the same theory that the ELO is. Here's a pretty graph =) It's properly centered at 1600 as well, unlike our glicko2 implementation which it seems has drifted - 50APS doesn't line up with 1600 like it used to (perhaps due to more strong bots re-submitted like MN was saying).

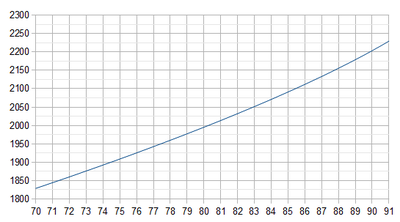
Hey that's not bad! It places some of the top 20 a bit high, and that bugs me a little, but every other bot fits a bit better.

My biggest worry is it places YersiniaPestis and up in the 2100's and Tomcat is very close to the 2200 (not really a problem), and the top 2 are over halfway to the 2300s (not a problem really, since they are in their own little universe anyway).

Traditionally the 2100's started around Phoenix (85.78), but Shadow (84.69) up would be perfectly fine.

-290*ln(100/APS - 1) + 1600

Might be a better compromise.

If you take a look here it seems that the APS has actually drifted as well.

The same version of Dookious, 1.573c had APS 85.65 on 2011/03/14, currently at 86.31. I can only conclude that lots of weaker bots must have been added to the rumble. I based that formula off of the old APS-->glicko2 relationship, and if the current APS has drifted due to weak bots being added I'm not sure if we should correct for that in our formula or not. It's a tough call.

While there is no simple way to take care that drift in the long run (that I can think of), I think we should correct it as much as we can at the moment. At least to a point where the current historical numbers have some meaning again (2000 club, etc). So at least people can claim their titles.

I would like to see a way to make the approximate elo a bit more drift tolerant, but I have no (good) suggestions on how to go about doing that.

We could just retire the clubs and make new APS ones. I'm as proud of 90 APS as any of my ELO club memberships. :-)

Yeah, considering that 80% lines up pretty well with what 2000 used to be I think this is a pretty good idea. Good luck with getting your power back, hope you didn't lose anything to Sandy =)

APS has no direct relationship to ELO. The APS can go up because, as you said, a lot of weak bots were added. For ELO not the pure result counts, but the result relative to the 'expected' result. If f.e. the expected result is 95-5, and the true result is too, ELO would not change, while APS will go up. For me, an ELO of 2000 for cf.proto.Shiva 2.2 would be acceptable, as it hoovered there in 2006-2008 (source: The 2000 Club). That means that -280 would be even a better pick in my opinion. Ofcourse that would not be ideal for every bot, but I think that setting the border for The 2000 Club as it used to be (long time ago) is a good compromise.

Aargh, forget what I said. This approximate ELO is direct related to APS. Still have the old ELO in my head. My remark about the border of The 2000 Club still stands though.

Personally, I don't consider changes to APS to be "drift", but just valid changes to overall score based on the rumble population. There is no such thing as an absolute rating, even with a (theoretical) perfectly designed ELO. To me, rating drift is a change in rating when the pair wise scores have not changed.

I haven't examined the data closely (4th day without power here!), but fwiw Dookious maxed at about 2130 on the old server and Komarious was almost exactly 2000.

You make a good argument, it isn't drift per say. I suppose we could go with this version of the AELO. Unlike APS its numbers are more `memorable`. Mostly because their larger, but also because of the logarithmic scaling at the extremes.

So instead of saying i'm ranked 90.2 vs 90. It is 2244 vs 2237. Besides, if you hit 100% you get to say you hit infinity.

There is a way to make an "absolute" rating in ELO, using an anchor competitor.

Choose one competitor, preferably a competitor which is never re-submitted, and define arbitrarily which rating it has. Then, modify rating updates so this anchor competitor rating never changes. All other competitors ratings will adjust in relation to the anchor competitor, instead of in relation to newer competitors added to the ranking.

I saw it been done in CGOS ranking.

But simply centering everyone around 1600 (ELO) or 50% (APS) is good enough for me.

I think that's a good idea, and is something David Alves had slated for roborumble.org =), but everyone else's ratings would still change as the population changes, just as APS does. I was just saying that is unavoidable, and not an anomalous side-effect of some weird scoring formula, like ELO rating drift.

Avoiding ratings drifts due to population increase is hard to workaround, and the anchor competitor is the only way I know.

But avoiding ratings drifts due to re-submits (everyone´s rating going down) can be avoided by centering everyone around a constant number, like 1600, or around a single anchor competitor.

If I had to pick an anchor, I would go with something like SandboxDT, RaikoMX or some other classic robot.