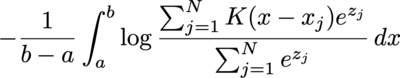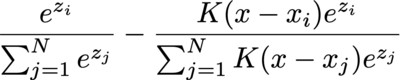Property of gradient of cross-entropy loss with kernel density estimation

I'm quite curious about the behavior of cross entropy loss between a uniform distribution and kernel density estimation with softmax weight:

where a and b is the lower and upper bound of the target uniform distribution, K is the kernel function (assume normalized), x_j is the angle of the data point, and z_j the weight before softmax.

The integral is often calculated by numerical methods, such as binning, so let's consider the gradient of the i-th data point's weight before softmax, and consider only one of the bins (with angle x) and ignore the values multiplied before integral:

It degenerates to ordinary cross entropy loss with softmax when K is either 1 or 0 (and 1 iif the "label" matches): S_i - 1 when label matches or S_i when label mismatches.

But things start to get interesting when K is different.

The thoughts on surfing & targeting is quite inspiring. And even if no data points are near within K size (hard case), that case is still valuable, since there may exist some data point just outside of the K size. And repeating the training process with new weight iteratively may eventually turn that case into an easy case ;) Are you doing something similar as well?

One more finding. Actually you don't need to take integral or use bins at all, you can compute the loss from each data point separately and take the sum of the loss. Although the value in loss isn't equal, the gradients are exactly the same. This yields one more insight: the absolute predicted value isn't important at all, all that matters is how relatively they are close to the target distribution, compared to each other. As a result, the cluster used for one prediction isn't necessarily in the same batch, they can be shuffled entirely, yet doesn't affect the result (theoretically).

Oops the calc is wrong.