Thread history

Squaring does not affect the order of nearest points, then with knn the same data points should be chosen.

And about noice

euclidean seems to be even more tolerant when noice has less energy than the main dimensions.

So manhattan seems to be more "elite-oriented", dropping points with offsets in another dimension more aggressively.

Anyway, according to https://datascience.stackexchange.com/questions/20075/when-would-one-use-manhattan-distance-as-opposite-to-euclidean-distance

Manhattan distance (L1 norm) may be preferable to Euclidean distance (L2 norm) for the case of high dimensional data:

Suppose there are 3 data points:

1 reference data point:

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

And 2 data points in the database:

[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] (Euclidean distance = 3.87, Squared Euclidean distance = 15, Manhattan distance = 15)

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4] (Euclidean distance = 4, Squared Euclidean distance = 16, Manhattan distance = 4)

If noise changes a single 0 into a 4, it will affect Euclidean distance 4x times higher than Manhattan distance. Euclidean distance will pick the first, Manhattan distance will pick the second.

this is a good demonstration! euclidean is sensitive to outliners and prefer the averagely non-bad one rather than some good point with some dimensions being noise.

Shouldn´t you be adding that +1 to the x value before squaring?

Euclidean distance = sqrt( (x+1)^2 )

Manhattan distance = | x+1 |

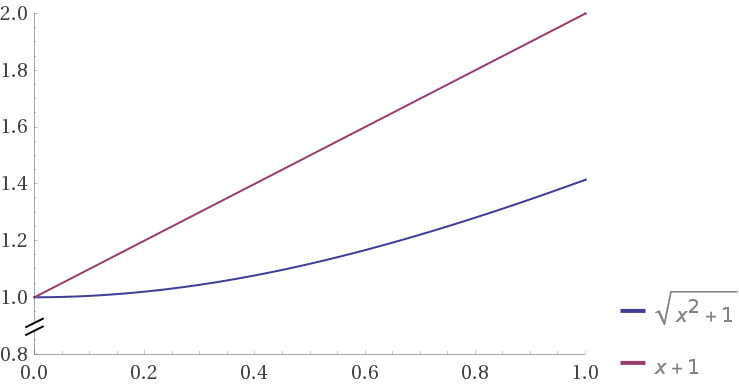
my case is noise in another dimension ;)

however if noise is added to the main dimension,

it will be

sqrt((1 + x)^2 + 1)

vs

|1 + x | + 1

and if we put two curves together (shifted so that tey intersects on x=0)

http://robowiki.net/w/images/5/5a/C3BD3E15-EEB6-4F63-826F-7C1F5E54A78E.gif

euclidean looks terrible with large noise in one dimension, and manhattan looks robust.