Reason behind using Manhattan distance

Distance Function Comparison in ML

The conversation is about the use of different distance functions in machine learning, specifically in the context of a gun for a video game. The participants discuss the use of Euclidean distance, Manhattan distance, and a log-based distance function. They mention that Manhattan distance performed better in the context of the game, and suggest that this may be due to the noise rejection properties of Manhattan distance and the curse of dimensionality in high-dimensional spaces. They also discuss the similarities between the L1 and L2 distance functions and the L1 and L2 norms in logistic regression and the idea of pattern matching with L1 norm.

— ChatGPT

In this page, I noticed

 using Euclidean distance decreased my score against real-world targets considerably

However, having better score is just a result instead of reason. And I've been thinking about the reason why Manhattan works better for years...

Today, something come to my mind. For faster calculation, most of us use SqrEuclidean instead of real Euclidean. This wouldn't affect the order, but once u use squared distance for gaussian function, boom, the actual distance (to the same degree as the Manhattan one) is squared twice, which actually decreases k size dramatically in some cases.

So could you remember whether your Euclidean version gun is using SqrEuclidean and using that (squared distance comparing to Manhattan) for gaussian, or the correct Euclidean distance is used for gaussian?

That was quite a while ago :-) But I know I tested a lot of different distance functions, including exotic things like multiplicative and log-based, and Manhattan worked best. I'm fairly sure I used Euclidean with a sqrt on the squared distance.

Having a gun that is different from what people expect is helpful, since the tuning they do doesn't affect you as much. This is my guess why Manhattan worked best for me

being different sounds reasonable, since there are plenty of vcs surfers (and vcs is more like euclidean than manhattan imho. btw i’m curious about what log-based distance function is ;)

Log based was something like log(1+abs(a1-b1))

Just had a thought about DrussGT's hundreds of random VCS bins and Manhattan distance —

Consider we have infinite amount of random VCS buffers (random bin size and dimensions, weighted equally, no decay), then 1 distance increment in a dimension result in "1" decrease in the total of buffers (data weight) containing that data.

When distance increased in dimension A by 1, and distance increased in dimension B by 1 as well, then data weight decreased by 1 + 1 = 2, in the same way manhattan distance works.

If we use manhattan distance together with knn, and decrease weight linearly on data distance, it should yield similar result to random VCS.

However, once rolling average (decay) is used, things get a lot different there...

I have 2 hypotheses:

- Manhattan distance is more tolerant to noise than Euclidean distance. Squaring a dimension amplifies noise.

- Curse of dimensionality. Euclidean distance behaves oddly at high dimensions.

Squaring does not affect the order of nearest points, then with knn the same data points should be chosen.

And about noice

euclidean seems to be even more tolerant when noice has less energy than the main dimensions.

So manhattan seems to be more "elite-oriented", dropping points with offsets in another dimension more aggressively.

Anyway, according to https://datascience.stackexchange.com/questions/20075/when-would-one-use-manhattan-distance-as-opposite-to-euclidean-distance

Manhattan distance (L1 norm) may be preferable to Euclidean distance (L2 norm) for the case of high dimensional data:

Suppose there are 3 data points:

1 reference data point:

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

And 2 data points in the database:

[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] (Euclidean distance = 3.87, Squared Euclidean distance = 15, Manhattan distance = 15)

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4] (Euclidean distance = 4, Squared Euclidean distance = 16, Manhattan distance = 4)

If noise changes a single 0 into a 4, it will affect Euclidean distance 4x times higher than Manhattan distance. Euclidean distance will pick the first, Manhattan distance will pick the second.

this is a good demonstration! euclidean is sensitive to outliners and prefer the averagely non-bad one rather than some good point with some dimensions being noise.

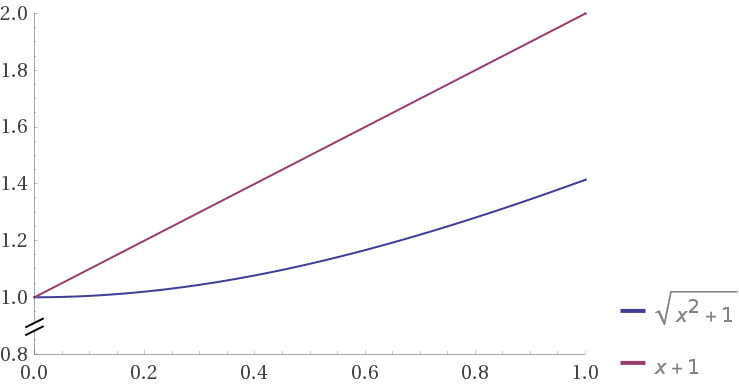
Shouldn´t you be adding that +1 to the x value before squaring?

Euclidean distance = sqrt( (x+1)^2 )

Manhattan distance = | x+1 |

my case is noise in another dimension ;)

however if noise is added to the main dimension,

it will be

sqrt((1 + x)^2 + 1)

vs

|1 + x | + 1

and if we put two curves together (shifted so that tey intersects on x=0)

http://robowiki.net/w/images/5/5a/C3BD3E15-EEB6-4F63-826F-7C1F5E54A78E.gif

euclidean looks terrible with large noise in one dimension, and manhattan looks robust.

I think it is due to the noise rejection. For me it is the ratio between how a small change in a lot of dimensions is weighted compared to a big change in a single dimension, as you demonstrated above. You can also think about it like the difference between L1 and L2 distance, how they would affect a minimization problem. L1 rejects large noises, and is the most robust you can get while still maintaining a convex search space. L2 has a gradient that gets larger the bigger the distance, so dimensions with more error are effectively weighted higher, and weighted higher than just proportional to the amount of error.

Rethinking this after 4.5 years, L1/L2 distancing resembles L1/L2 norm in logistic regression, where L1 norm tend to find weights with more zeros, and L2 norm tend to find equal but non-zero weights for co-linear attributes. Since no one is using duplicated attributes due to limited dimensionality, this benefit of L2 norm is nullified.

The property of having more zeros of L1 norm reminds me of pattern matching, where zero means a match and non-zero means a mismatch. Being able to make a partial but best-effort match effectively simulates using a large amount of trees, eaching having a subset of the attributes.