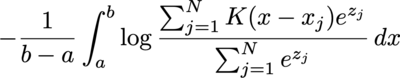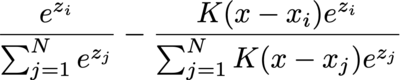Property of gradient of cross-entropy loss with kernel density estimation

I'm quite curious about the behavior of cross entropy loss between a uniform distribution and kernel density estimation with softmax weight:

where a and b is the lower and upper bound of the target uniform distribution, K is the kernel function (assume normalized), x_j is the angle of the data point, and z_j the weight before softmax.

The integral is often calculated by numerical methods, such as binning, so let's consider the gradient of the i-th data point's weight before softmax, and consider only one of the bins (with angle x) and ignore the values multiplied before integral:

It degenerates to ordinary cross entropy loss with softmax when K is either 1 or 0 (and 1 iif the "label" matches): S_i - 1 when label matches or S_i when label mismatches.

But things start to get interesting when K is different.

Interesting observations! The scale invariance of K actually seems like a good property to me. It means that K doesn't really need to be normalized, or more precisely that multiplying K by a constant multiplies the gradient by that constant, which seems like the behavior you'd want. Most loss functions (e.g., mean squared error) learn more for far data points than close ones. That might be good for surfing, but I could imagine that you may want the opposite for targeting where you "give up" on hard data points and focus on the ones that you might score a hit on. So perhaps BeepBoop's loss is a middle ground that works decently well for both.

The thoughts on surfing & targeting is quite inspiring. And even if no data points are near within K size (hard case), that case is still valuable, since there may exist some data point just outside of the K size. And repeating the training process with new weight iteratively may eventually turn that case into an easy case ;) Are you doing something similar as well?