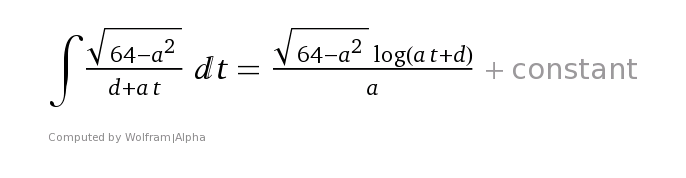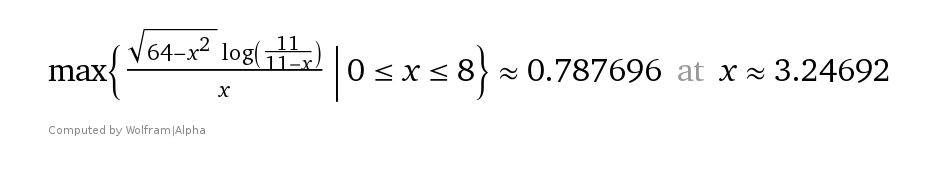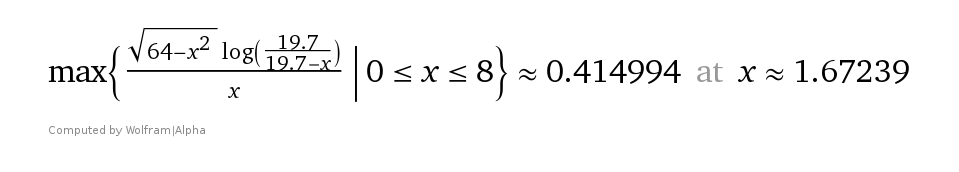Difference between revisions of "User:Xor/Better MEA formula"

From Robowiki
Jump to navigation Jump to search
m (backup)
m (fix)
 
(17 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
[[File:BetterMEA.gif]]
+
After all, I think the traditional MEA is theoretically correct. And I have a proof that is too large to fit in the margin ;).  
  
−
Where x is Bullet Speed.
+
----
  
−
A better MEA can be archived when moving at a lateral speed of [[File:LateralVelocityForMEA.gif]] (and moving away (at max retreat velocity) at the same time definitely)
 
  
−
Note: by formula, I mean theoretical (ignoring acceleration & wall), as Precise Game Physics can never be covered by one single formula.
+
It seems that I made a mistake in previous calculation.  
  
 +
Correct calculation —
  
−
== Proof ==
+
Consider a situation when you move orbital to the source of the wave with constant retreat angle (therefore constant lateral velocity and retreat velocity) —
  
−
Asuming you are moving in constant lateral velocity, and max velocity. And ignore acceleration & wall.  
+
[[File:IntegralBetterMEA.png]]
  
−
Then
+
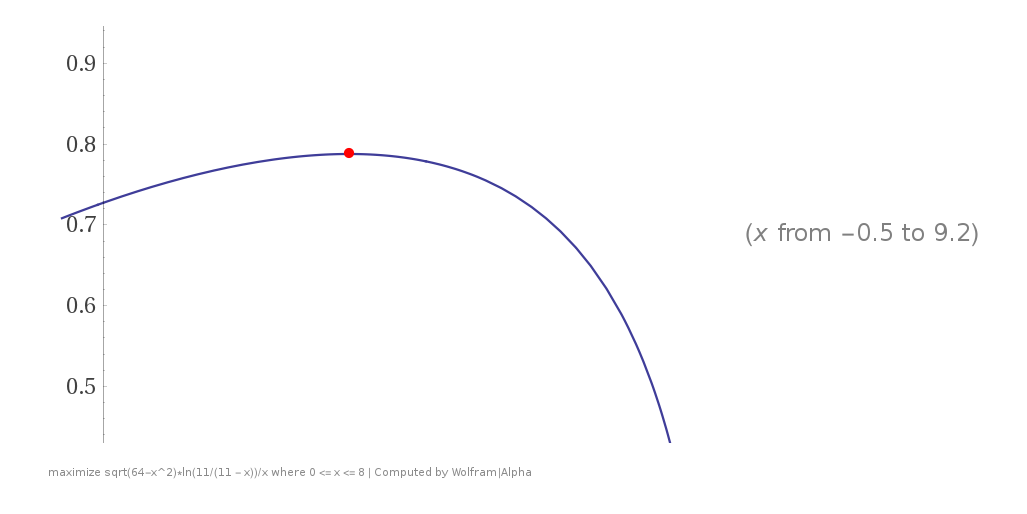
[[File:BetterMEABulletSpeed11.png]]
 +
 
 +
[[File:BetterMEAResultBulletSpeed11.png]]
 +
 
 +
where x is retreat velocity (the negative of advancing velocity)
 +
 
 +
However this formula is not greater than the traditional one ;/
 +
 
 +
Sorry guys.
 +
 
 +
 
 +
Anyway, unlike traditional MEA which you can use for only one wave — this formula is capable of being used to maximize escape angle of every wave. Therefore it is still better — useful for wave surfers.
 +
 
 +
The best retreat angle (for power 3.0 bullet, considering only MEA) is — 1.152871236rad. (where moving away directly is 0rad)
 +
 
 +
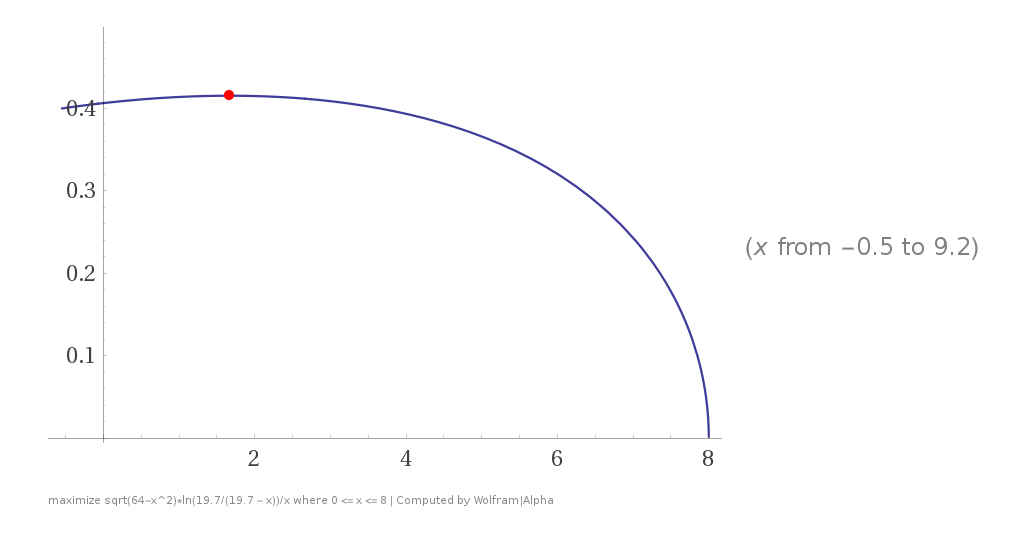
[[File:BetterMEABulletSpeed19_7.png]]
 +
 
 +
[[File:BetterMEAResultBulletSpeed19_7.png]]
 +
 
 +
And for 19.7 wave speed — the result is mea = 0.414994rad, while the traditional one is 0.418172793rad. Pretty close though? (0.1821°) And you can do that for every wave! (until you hit the wall ;) )
 +
 
 +
The best retreat angle for power 0.1 bullet (considering only MEA) is 1.360194211rad. (where moving away directly is 0rad)

Latest revision as of 10:15, 18 September 2017

After all, I think the traditional MEA is theoretically correct. And I have a proof that is too large to fit in the margin ;).


It seems that I made a mistake in previous calculation.

Correct calculation —

Consider a situation when you move orbital to the source of the wave with constant retreat angle (therefore constant lateral velocity and retreat velocity) —

IntegralBetterMEA.png

BetterMEABulletSpeed11.png

BetterMEAResultBulletSpeed11.png

where x is retreat velocity (the negative of advancing velocity)

However this formula is not greater than the traditional one ;/

Sorry guys.


Anyway, unlike traditional MEA which you can use for only one wave — this formula is capable of being used to maximize escape angle of every wave. Therefore it is still better — useful for wave surfers.

The best retreat angle (for power 3.0 bullet, considering only MEA) is — 1.152871236rad. (where moving away directly is 0rad)

BetterMEABulletSpeed19 7.png

BetterMEAResultBulletSpeed19 7.png

And for 19.7 wave speed — the result is mea = 0.414994rad, while the traditional one is 0.418172793rad. Pretty close though? (0.1821°) And you can do that for every wave! (until you hit the wall ;) )

The best retreat angle for power 0.1 bullet (considering only MEA) is 1.360194211rad. (where moving away directly is 0rad)

Retrieved from "http://robowiki.net/w/index.php?title=User:Xor/Better_MEA_formula&oldid=51954"