Difference between revisions of "Zoom Radar"
m (Reduced code size by optimizing layout.) |
m (Revised LaTeX after Voidious fixed!) |
||
| Line 110: | Line 110: | ||
<TR> | <TR> | ||
<TD> | <TD> | ||
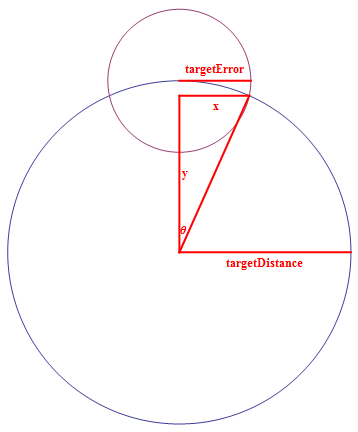
| − | <MATH>\angle\ | + | <MATH>\angle\theta_\text{Bounding} = \tan ^{-1}\left(\frac{x}{y}\right)</MATH> |
</TD> | </TD> | ||
<TD ROWSPAN="2"> | <TD ROWSPAN="2"> | ||
| Line 155: | Line 155: | ||
<TR> | <TR> | ||
<TD> | <TD> | ||
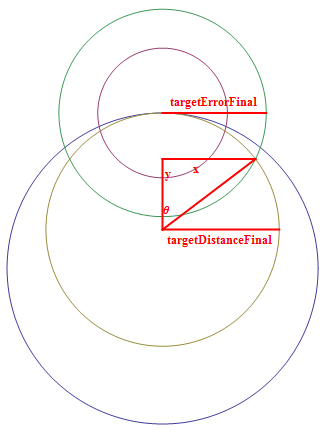
| − | <MATH>\angle\ | + | <MATH>\angle\theta_\text{Final} = \tan ^{-1}\left(\frac{x}{y}\right)</MATH> |
</TD> | </TD> | ||
<TD ROWSPAN="2"> | <TD ROWSPAN="2"> | ||
Revision as of 19:39, 26 February 2010
Zoom radar is a precise lock radar with a minimum cost feature for melee. Created by Frolicking Zombie.
When the radar's bearing is between the thetaBounding and thetaFinal bearings, this signals the completion of the scan in the corresponding direction. The scan direction should be reversed to (re)cover the target area. When a target has been scanned, the radar must reverse direction to ensure a scan on the next subsequent turn. This enables a precision lock on the target. The variable lastScanDirection should be initialized with the value that corresponds to the direction (1 = CW, -1 = CCW) of the scan used to find all targets. The variable scanDirection should be initialized with 0 to force a new search. When initiating a new search, if it is determined that the CW and CCW scans will be equal, the direction of search should be the one that will scan the most targets along the path to the desired target.
// Bearings are negative in the CCW direction.
if(scanDirection == -1) {
// Check to see if we have completed our move.
if(radarBearing >= -thetaFinal && radarBearing <= -thetaBounding) {
// Should have scanned target by now. Resume in opposite direction
scanDirection = 1;
}
else {
// Continue in the CCW direction.
scanDirection = -1;
}
}
else if(scanDirection == 1) {
// Check to see if we have completed our move.
if(radarBearing <= thetaFinal && radarBearing >= thetaBounding) {
// Should have scanned target by now. Resume in opposite direction
scanDirection = -1;
}
else {
// Continue in the CW direction.
scanDirection = 1;
}
}
// Set scanDirection = 0 if we just scanned the target we were looking for so that we can continue scanning in the most manner.
else {
// Check to see if we are within bounds.
if(radarBearing >= -thetaBounding && radarBearing <= thetaBounding) {
// Start scanning in the opposite direction to ensure that we scan the target on this turn.
scanDirection = lastScanDirection * -1;
}
// Check to see if the CW bound is closer.
else if(Math.abs(thetaFinal - radarBearing) < Math.abs((-thetaFinal) - radarBearing)) {
// Scan in the CCW direction ending at the CCW bound.
scanDirection = -1;
}
// Check to see if the CCW bound is closer.
else if(Math.abs(thetaFinal - radarBearing) > Math.abs((-thetaFinal) - radarBearing)) {
// Scan in the CW direction ending at the CW bound.
scanDirection = 1;
}
// Both bounds are equal.
else {
// Add code here....
// Just count the number of targets you expect to scan along the CW and CCW directions and start scanning in the most advantageous direction.
if(targetsCW >= targetsCCW) {
scanDirection = 1;
}
else {
scanDirection = -1;
}
}
}
setTurnRadarRightRadians((scanDirection * thetaFinal) – radarBearing);
lastScanDirection = scanDirection;
If <MATH>2 \times \text{targetDistanceFinal} < \text{targetErrorFinal}</MATH> then it will be impossible to resolve bearings that the target may not be at. It is best to continue scanning in the same direction as previous, but with no bounds.
if(2 * targetDistanceFinal < targetErrorFinal) {
scanDirection = lastScanDirection;
setTurnRadarRightRadians(scanDirection * 2* Math.PI);
}