Talk:Zoom Radar
There seems to be a lot of errors regarding rendering LaTeX. Is there a way to resolve this? --Frolicking Zombie 17:53, 26 February 2010 (UTC)
Ok, I'm looking into it... --Voidious 18:08, 26 February 2010 (UTC)
Fixed:
- <math>
it = {{works - now} \over {\Delta Friday}} </math> Enjoy. =) --Voidious 18:33, 26 February 2010 (UTC)
Some comments
Heh, actually, inspired by what you had on your talk page, though doing the math a bit different, I've already implemented something along these lines in Glaicer. Take a look at Glacier's "ags.muse.radar.MeleeRadar" class, which IMO is much cleaner. It also looks really spiffy in action. Also, the math here is wrong, in that one gets the most change in angle by moving along a chord of the circle created by the distance to the enemy bot, and that fact also simplifies the math to calculate the uncertainty in angle to the following:
double maxMoved = rules.MAX_VELOCITY*bot.getDataAge();
double uncertainty;
if (distance * 2 > maxMoved) {
uncertainty = 2*Math.asin(maxMoved/(2*distance));
}
else {
uncertainty = Math.PI;
}Essentially a single arcsine with a special condition for when they haven't been seen in so long that their angle is completely unknown (i.e. could be PI radians different in either direction).
Another note, is that in order to be accurate enough to ensure you don't slip when being this precise, it's also necessary to count the change in radar origin position caused by one's own movement.
Also, why the name "Zoom Radar"? I don't see any "zooming". --Rednaxela 17:54, 26 February 2010 (UTC)
The triangle formed in your equation would be the equivalent as if the robot traveled along the tangent created by the targetDistance circle. This creates slightly less of an angle (which promotes slip) than if you calculate the intercept of the targetError and targetDistance circles. BTW, why would you use (2*distance) as the hypotenuse of your triangle? --Frolicking Zombie 18:13, 26 February 2010 (UTC)
I think you're mis-visualizing the geometry of my equation, but I think that's my fault. (2*distance) isn't a hypotenuse, and it's made of two triangles, not one. I probably should have wrote it as "uncertainty = 2*Math.asin((maxMoved/2)/distance);" but I was silly and didn't (I really need to get out of my habit of pointless premature micro-optimizations (in this case to do with how multiplication is faster than division)). To get a better idea what it means, see the following diagram that I quickly whipped up:
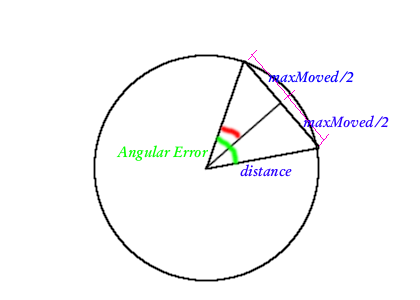
Moving across the chord of the circle is truly the fastest way to for the enemy to change angles. After all, what's the quickest way for an enemy bot to change it's angle by 180 degrees? Just drive straight to the other side of you. --Rednaxela 19:18, 26 February 2010 (UTC)
I understand your method better with the picture. Both methods will end up with the same result, but yours is less computationally intensive to retrieve the bearing. /me bows. Mind if I update the code to reflect your method? --Frolicking Zombie 19:26, 26 February 2010 (UTC)
Feel free to... but just now I realized that the assumption of the chord being the most efficient path to change angle is incorrect. It's typical, so works well in practice as Glacier shows, but the real uncertainty factor is actually larger. To change angle, it's actually more efficiency to dive towards the enemy, plus if one drives straight towards the enemy, the angle will change by 180 degrees after traveling (distance) not (2*distance) right through where the bot is. It should be follows I now realize:
double maxMoved = rules.MAX_VELOCITY*bot.getDataAge();
double uncertainty;
if (distance >= maxMoved) {
uncertainty = Math.asin(maxMoved/distance);
}
else {
uncertainty = Math.PI;
}to be really safe... in order to tighten it any further than that, and give any guarantees, requires relying on acceleration limits of bots or that they must be at least 'botWidth' distance from you currently. --Rednaxela 19:42, 26 February 2010 (UTC)
I can see now that both of our methods assumed that the target would be orbiting and maintaining itself perpendicular. If you looked at the graphic, the presence of a chord clearly indicates that there are places that the target could travel that would result in greater bearings. The max bearing would be the angle that is tangent, which the angle for is asin(targetError/targetDistance). --Frolicking Zombie 21:31, 26 February 2010 (UTC)
- Yes, that's what I was trying to say. I'm now working on an improved version to be able to narrow the uncertainty further by considering that you only need to see the edge of the robot rather than the center of it in order to detect it. This should give an even more efficient result in most circumstances, than the old one that used the bad assumptions we made, but still safe in the extreme conditions our old methods were not safe for. --Rednaxela 00:53, 27 February 2010 (UTC)
I may be talking out my ass here, not having followed your entire conversation closely, but you may need to double your expected angles, and here is why: Let's say for the sake of argument that your opponent is somewhere above you. Turn 105, you move, he moves, and you sweep your radar over him counterclockwise. You are told his position in turn 106. You anticipate that the furthest he can move to the right places him just left of true north, so you sweep to 0 radians, minimizing the width of your sweep and looking really slick with your narrow beam. Turn 106 is processed: you move, he moves, you sweep right, and now he is just left of your radar. So.. do you sweep left, or right? Left seems obvious .. he's to the left. But before you turn your radar, he is going to move. If he moves to the right of your radar beam, then you sweep left, your radar lock just slipped. If you sweep right and he slows down enough (possibly with the help of a solid object), your radar lock may slip to the right. If you instead sweep twice as far as he could move at full speed, there will never be a question of slipping due to anticipating velocity. It's not as absolutely cool as it could be, but honestly radar just needs to work. How many people watch battles with the radar graphic enabled anyway? --Martin 23:58, 26 February 2010 (UTC)
- The details of Glacier's radar fully consider this issue I believe. Also about the usefulness of fancy radar... Glacier currently is able to keep a better don't-miss-a-tick lock on two widely separated bots better than any other melee bot currently in the field, and a barely-miss-any-ticks lock on two even wider separated bots by taking advantage of boosting the max radar rotation using the gun turret when gunheat is high. It's not worth much score, but it should really help bullet detection for melee surfing and such. Also, I always watch with radar graphics personally, even when I'm not experimenting with it :P --Rednaxela 00:53, 27 February 2010 (UTC)
- [View source↑]
- [History↑]