Difference between revisions of "Escape Circle"
(Initial commit) |
(Add calculation section) |
||
| Line 1: | Line 1: | ||
| − | + | '''Escape Circle''' is the circumference of [[Escape Envelope]] assuming the motion of the target is linear and uniform. | |
| + | |||
| + | == Calculation == | ||
[[File:EscapeCircle.png|600px]] | [[File:EscapeCircle.png|600px]] | ||
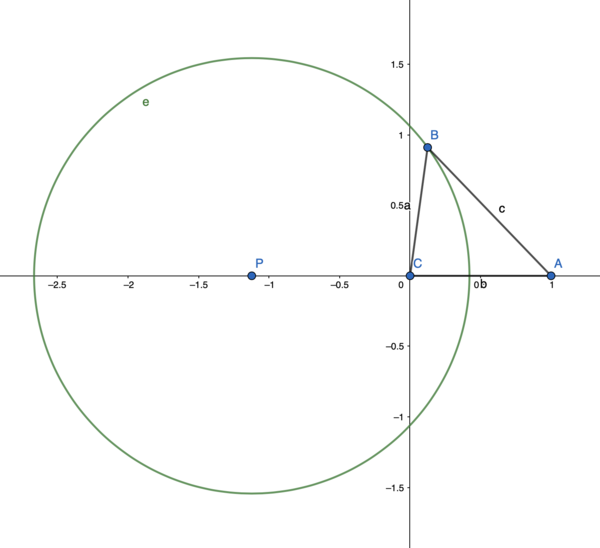
| − | + | Assuming uniform linear motion, consider a situation where a bullet fired from the firer A hits the target C at some future position B. A is the angle opposite to a, B is opposite to b, and C is opposite to c. | |
| + | |||
| + | Let the target C be the origin, the distance and orientation from the target to the firer be the unit length and positive x-axis respectively. | ||
| + | |||
| + | Let θ be the angle between b and a, we have c / a = Vb / Vr, b = 1, where Vb and Vr is the velocity of the bullet and the target respectively. Now consider cosine formula: | ||
| + | |||
| + | a<sup>2</sup> + 1<sup>2</sup> - 2 a cosθ = (Vb / Vr a)<sup>2</sup> | ||
| + | |||
| + | Let x = a cosθ, y = a sinθ, k = 1 / ((Vb / Vr)<sup>2</sup> - 1), we have: | ||
| + | |||
| + | (x + k)<sup>2</sup> + y<sup>2</sup> = k<sup>2</sup> + k | ||
| + | |||
| + | The points defined by (x, y) satisfying above formula is a circle e with center P(-k, 0), and radius sqrt(k<sup>2</sup> + k). | ||
== See also == | == See also == | ||
Revision as of 09:17, 8 August 2019
Escape Circle is the circumference of Escape Envelope assuming the motion of the target is linear and uniform.
Calculation
Assuming uniform linear motion, consider a situation where a bullet fired from the firer A hits the target C at some future position B. A is the angle opposite to a, B is opposite to b, and C is opposite to c.
Let the target C be the origin, the distance and orientation from the target to the firer be the unit length and positive x-axis respectively.
Let θ be the angle between b and a, we have c / a = Vb / Vr, b = 1, where Vb and Vr is the velocity of the bullet and the target respectively. Now consider cosine formula:
a2 + 12 - 2 a cosθ = (Vb / Vr a)2
Let x = a cosθ, y = a sinθ, k = 1 / ((Vb / Vr)2 - 1), we have:
(x + k)2 + y2 = k2 + k
The points defined by (x, y) satisfying above formula is a circle e with center P(-k, 0), and radius sqrt(k2 + k).