Difference between revisions of "Maximum Escape Angle/Precise Positional/Non-Iterative"
(Initial commit) |
m (clean) |
||
| Line 13: | Line 13: | ||
(x + c)<sup>2</sup> + 2 c x = 1<sup>2</sup> (c<sup>2</sup> + c) | (x + c)<sup>2</sup> + 2 c x = 1<sup>2</sup> (c<sup>2</sup> + c) | ||
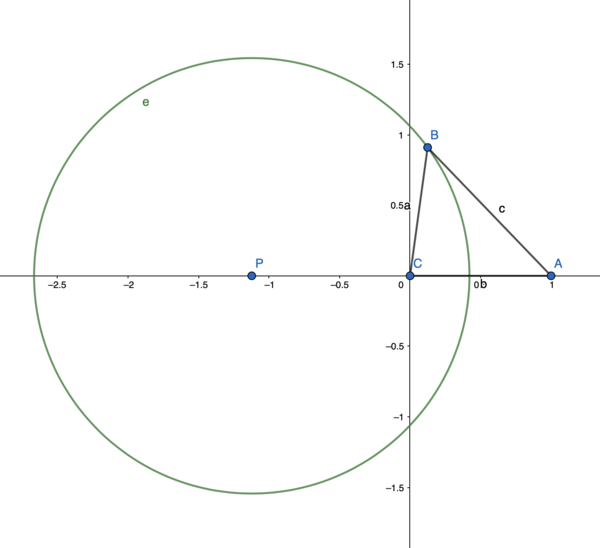
| − | The points defined by (x, y) satisfying above formula is a circle e with center | + | The points defined by (x, y) satisfying above formula is a circle e with center = P(-c, 0), and radius = sqrt(c<sup>2</sup> + c). |
| − | To find precise positional max escape angle, select the max of the escape angles calculated from | + | To find precise positional max escape angle, select the max of the escape angles calculated from the intersections of the above circle and the walls, or use traditional max escape angle when no intersection can be found. |
Revision as of 15:18, 6 August 2019
Consider a situation where a bullet fired from the firer A hits the target C at some future position B. A is the angle opposite to a, B is opposite to b, and C is opposite to c.
Let the target C be the origin, the distance and orientation from the target to the firer be the unit length and positive x-axis respectively.
Let θ be the angle between b and a, we have c / a = Vb / Vr, b = 1, where Vb and Vr is the velocity of the bullet and the target respectively. Now consider cosine formula:
a2 + 12 - 2 a cosθ = (Vb / Vr a)2
Let x = a cosθ, y = a sinθ, c = 1 / ((Vb / Vr)2 - 1), we have:
(x + c)2 + 2 c x = 12 (c2 + c)
The points defined by (x, y) satisfying above formula is a circle e with center = P(-c, 0), and radius = sqrt(c2 + c).
To find precise positional max escape angle, select the max of the escape angles calculated from the intersections of the above circle and the walls, or use traditional max escape angle when no intersection can be found.