Difference between revisions of "Escape Circle"
m (add condition) |
(Add example code for calculation Escape Circle) |
||
| Line 18: | Line 18: | ||
The points defined by (x, y) satisfying above formula is a circle e with center P(-k, 0), and radius sqrt(k<sup>2</sup> + k). | The points defined by (x, y) satisfying above formula is a circle e with center P(-k, 0), and radius sqrt(k<sup>2</sup> + k). | ||
| + | |||
| + | == Example code == | ||
| + | |||
| + | <syntaxhighlight> | ||
| + | import java.awt.geom.Point2D; | ||
| + | |||
| + | public final class EscapeCircle { | ||
| + | public Point2D.Double center; | ||
| + | public double radius; | ||
| + | |||
| + | public EscapeCircle(Point2D.Double center, double radius) { | ||
| + | this.center = center; | ||
| + | this.radius = radius; | ||
| + | } | ||
| + | |||
| + | public static EscapeCircle calc(Point2D.Double fireLocation, Point2D.Double targetLocation, double waveSpeed) { | ||
| + | double distance = fireLocation.distance(targetLocation); | ||
| + | double k = 1. / (sq(waveSpeed / 8.) - 1.); | ||
| + | double radius = distance * Math.sqrt(k * k + k); | ||
| + | |||
| + | return new EscapeCircle(scale(fireLocation, targetLocation, 1 + k), radius); | ||
| + | } | ||
| + | |||
| + | private static Point2D.Double scale(Point2D.Double origin, Point2D.Double point, double ratio) { | ||
| + | return new Point2D.Double( | ||
| + | origin.x + ratio * (point.x - origin.x), | ||
| + | origin.y + ratio * (point.y - origin.y) | ||
| + | ); | ||
| + | } | ||
| + | |||
| + | private static double sq(double x) { | ||
| + | return x * x; | ||
| + | } | ||
| + | } | ||
| + | </syntaxhighlight> | ||
== See also == | == See also == | ||
Revision as of 09:31, 8 August 2019
Escape Circle is the circumference of Escape Envelope assuming the motion of the target is linear and uniform, and ignoring any collision with walls or other robots.
Calculation
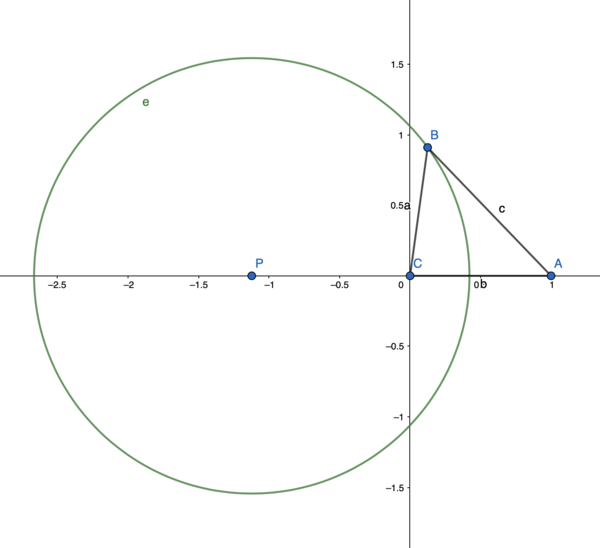
Assuming uniform linear motion, consider a situation where a bullet fired from the firer A hits the target C at some future position B. A is the angle opposite to a, B is opposite to b, and C is opposite to c.
Let the target C be the origin, the distance and orientation from the target to the firer be the unit length and positive x-axis respectively.
Let θ be the angle between b and a, we have c / a = Vb / Vr, b = 1, where Vb and Vr is the velocity of the bullet and the target respectively. Now consider cosine formula:
a2 + 12 - 2 a cosθ = (Vb / Vr a)2
Let x = a cosθ, y = a sinθ, k = 1 / ((Vb / Vr)2 - 1), we have:
(x + k)2 + y2 = k2 + k
The points defined by (x, y) satisfying above formula is a circle e with center P(-k, 0), and radius sqrt(k2 + k).
Example code
import java.awt.geom.Point2D;
public final class EscapeCircle {
public Point2D.Double center;
public double radius;
public EscapeCircle(Point2D.Double center, double radius) {
this.center = center;
this.radius = radius;
}
public static EscapeCircle calc(Point2D.Double fireLocation, Point2D.Double targetLocation, double waveSpeed) {
double distance = fireLocation.distance(targetLocation);
double k = 1. / (sq(waveSpeed / 8.) - 1.);
double radius = distance * Math.sqrt(k * k + k);
return new EscapeCircle(scale(fireLocation, targetLocation, 1 + k), radius);
}
private static Point2D.Double scale(Point2D.Double origin, Point2D.Double point, double ratio) {
return new Point2D.Double(
origin.x + ratio * (point.x - origin.x),
origin.y + ratio * (point.y - origin.y)
);
}
private static double sq(double x) {
return x * x;
}
}