Difference between revisions of "Escape Circle"
m (add ''Shape of the escape envelope'' to see also) |
m (Xor moved page EscapeCircle to Escape Circle: add space between title) |
(No difference)
| |
Revision as of 09:37, 8 August 2019
Escape Circle is the circumference of Escape Envelope assuming the motion of the target is linear and uniform, and ignoring any collision with walls or other robots.
Prove & calculation
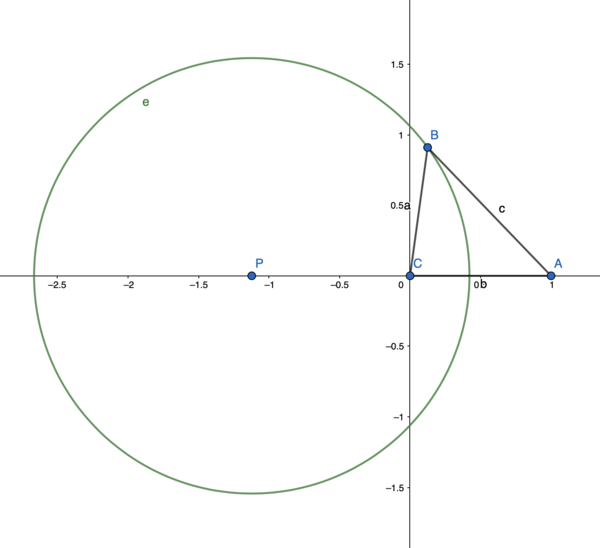
Assuming uniform linear motion, consider a situation where a bullet fired from the firer A hits the target C at some future position B. A is the angle opposite to a, B is opposite to b, and C is opposite to c.
Let the target C be the origin, the distance and orientation from the target to the firer be the unit length and positive x-axis respectively.
Let θ be the angle between b and a, we have c / a = Vb / Vr, b = 1, where Vb and Vr is the velocity of the bullet and the target respectively. Now consider cosine formula:
a2 + 12 - 2 a cosθ = (Vb / Vr a)2
Let x = a cosθ, y = a sinθ, k = 1 / ((Vb / Vr)2 - 1), we have:
(x + k)2 + y2 = k2 + k
The points defined by (x, y) satisfying above formula is a circle e with center P(-k, 0), and radius sqrt(k2 + k).
Example code
import java.awt.geom.Point2D;
public final class EscapeCircle {
public Point2D.Double center;
public double radius;
public EscapeCircle(Point2D.Double center, double radius) {
this.center = center;
this.radius = radius;
}
public static EscapeCircle calc(Point2D.Double fireLocation, Point2D.Double targetLocation, double waveSpeed) {
double distance = fireLocation.distance(targetLocation);
double k = 1. / (sq(waveSpeed / 8.) - 1.);
double radius = distance * Math.sqrt(k * k + k);
return new EscapeCircle(scale(fireLocation, targetLocation, 1 + k), radius);
}
private static Point2D.Double scale(Point2D.Double origin, Point2D.Double point, double ratio) {
return new Point2D.Double(
origin.x + ratio * (point.x - origin.x),
origin.y + ratio * (point.y - origin.y)
);
}
private static double sq(double x) {
return x * x;
}
}