User talk:Frolicking Zombie
|
Welcome! Hello, Frolicking Zombie, and welcome to RoboWiki! This place contains a wealth information about Robocode, from basic to more advanced. I hope you enjoy creating robots and being a robocoder! If you are posting a comment on this wiki, please sign your messages using four tildes (--~~~~); this will automatically insert your username and the date stamp. If you are not familiar with MediaWiki, these links might help you out:
If you need help, check out the frequently asked questions or ask it on this page. Again, welcome! —— Nat 15:07, 17 August 2009 (UTC) |
| Mathematics | RoboCode Java | Explanation |
|---|---|---|
|
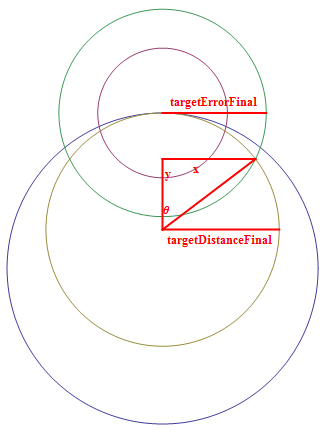
<math>\text{targetError} = (\text{currentTime} - \text{lastScanTime} + 1)\times 8 + 18</math> |
double targetError = (currentTime - targetLastScan + 1) * 8 + 18;
|
Calculate the maximum distance the enemy can possibly move according to the physics. |
|
<math>\text{targetDistance} = \sqrt{(\text{targetX} - \text{myX})^2+(\text{targetY}-\text{myY})^2}</math> |
double targetDistance = Math.sqrt(
(targetX - myX) * (targetX - myX) + (targetY - myY) * (targetY - myY)
);
|
Standard Euclidean distance formula for our distance to target. |
|
<math>\angle\text{targetHeading} = \tan ^{-1}\left(\frac{\text{targetY}-\text{myY}}{\text{targetX}-\text{myX}}\right)</math> |
double targetHeading = Math.atan2(targetX - myX, targetY - myY);
|
Robocode trigonometry has <math>\tan \theta = \frac{\cos \theta}{\sin \theta}</math> |
|
<math>\text{x = }\pm \frac{1}{2} \sqrt{4 \text{targetError}^2-\frac{\text{targetError}^4}{\text{targetDistance}^2}}</math>
|
double x = Math.sqrt(
targetError * targetError - (targetError * targetError * targetError * targetError)
/ (targetDistance * targetDistance)) / 2;
double y = (2 * targetDistance * targetDistance - targetError * targetError)
/ (2 * targetDistance);
|
The maximum angle that the enemy could have traveled is the intersection of the targetError and targetDistance circles. |
|
<math>\angle\theta\text{ = }\tan ^{-1}\left(\frac{x}{y}\right)</math> |
double theta = Math.atan2(y,x);
|
Calculate the maximum bearing that the enemy could have traveled. |
<math>\angle\text{cwBoundHeading} = \angle\text{targetHeading}+\angle\theta</math>
<math>\angle\text{ccwBoundHeading} = \angle\text{targetHeading}-\angle\theta</math>
Hey there! Wanna tell us what you're doing? Looks pretty interesting. =) « AaronR « Talk « 14:04, 16 August 2009 (UTC)
Looks really interesting... Do tell =) » Nat | Talk » 14:59, 16 August 2009 (UTC)
Hmm... looks like it's calculating some upper/lower bounds on the angle that an enemy bot could be at, in a melee environment where scans are infrequent --Rednaxela 16:20, 16 August 2009 (UTC)
Just working on this article over here before I move it. It's a minimal cost radar with some features for melee.