Talk:Maximum Escape Angle/Precise
Calculating
There was some discussion of this recently and I just read some more on User talk:Rednaxela/SaphireEdge, so I thought I'd post how it's done in Dookious and Diamond. Of course, trust your own findings on how valuable this is, but I have personally found precise MEA to be a good thing, both in TC and the rumble. All of these steps use Precise Prediction, just like in Wave Surfing.
- Simulate the enemy turning perpendicular to the wave's absolute bearing and accelerating to full speed. This is what
Math.asin(8.0 / bulletSpeed)approximates, but that of course ignores current speed and heading. Predict until the wave passes the enemy and calculate the resulting MEA. If the enemy didn't hit a wall, just use this, otherwise continue to the remaining steps. - Simulate the enemy moving perpendicular to the wave's abs bearing, but with Wall Smoothing. I use a wall stick of 80 and ignore wall hits (ie, use the wall to calculate how he will move, but let him move through walls).
- Repeat step 2 a second and third time, but instead of moving perpendicular, have the enemy move directly towards the point at which they ended the previous simulation. If the enemy will end at that spot, he can further increase his MEA by just heading straight toward that spot to begin with.
- The precise MEA returned is the maximum MEA from any of the above calculations.
This is all in Dookious/utils/Wave.java and Diamond/utils/DiaWave.java. In Diamond, I don't use this for GFs, but I use (precise MEA / traditional MEA) as the wall distance attribute, since I think wall distance is meant to tell you how much the wall is impacting the enemy's movement.
--Voidious 17:24, 18 September 2009 (UTC)
public LinkedList<Point2D> precisePrediction(Point2D me, Point2D them, double heading, double velocity, double bSpeed, int moveDir) {
LinkedList<Point2D> tmp = new LinkedList<Point2D>();
//Not entirely sure this time is set right, but if not, its very close. :)
int time = 0;
tmp.add(them);
do {
double absAngle = Tools.absoluteBearing(them, me);
double absAngle2 = Tools.absoluteBearing(me, them);
double latVelocity = velocity * Math.sin(heading - absAngle2);
int direction = Tools.sign(latVelocity);
//Best angle is perpendicular to the owner.
double targetAngle = absAngle - Math.PI / 2.0 * direction;
while(!battlefield.contains(Tools.project(them, targetAngle, 120))) {
targetAngle += 0.1*direction;
}
double turn = Utils.normalRelativeAngle(targetAngle - heading);
if(Math.abs(turn) > Math.PI / 2.0) {
turn = Utils.normalRelativeAngle(turn + Math.PI);
direction = -direction;
}
MovSim2Stat stat = MovSim2.step(them, velocity, direction*moveDir, heading, turn);
them = new Point2D.Double(stat.x,stat.y);
heading = stat.h;
velocity = stat.v;
++time;
tmp.add(them);
} while(bSpeed * time < me.distance(them));
return tmp;
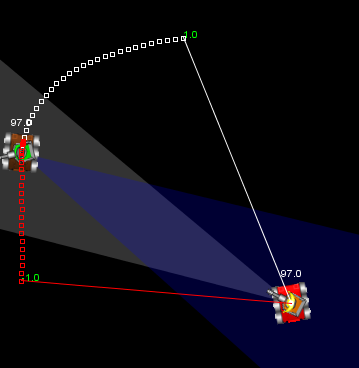
}To be fair Voidious implementing this can be quite a trick when you don't have a working Precise Predictor. I fixed that on mine, I used a stick of 120 in this image, but having read your comment here, I think I might try and lower it before I try it in actual use in my gun. — Chase-san 10:04, 7 July 2010 (UTC)
- [View source↑]
- [History↑]
You cannot post new threads to this discussion page because it has been protected from new threads, or you do not currently have permission to edit.