Escape Circle

Escape Circle is the circumference of Escape Envelope assuming the motion of the target is linear and uniform, and ignoring any collision with walls or other robots.

Prove & calculation

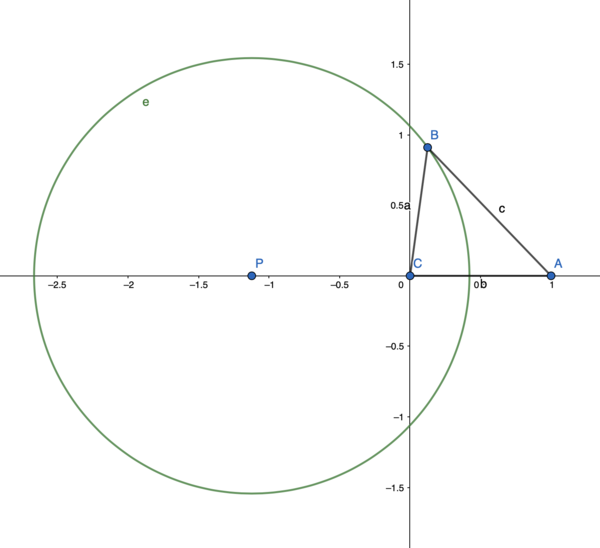
Assuming uniform linear motion, consider a situation where a bullet fired from the firer A hits the target C at some future position B. A is the angle opposite to a, B is opposite to b, and C is opposite to c.

Let the target C be the origin, the distance and orientation from the target to the firer be the unit length and positive x-axis respectively.

Let θ be the angle between b and a, we have c / a = Vb / Vr, b = 1, where Vb and Vr is the velocity of the bullet and the target respectively. Now consider cosine formula:

a² + 1² - 2 a cosθ = (Vb / Vr a)²

Let x = a cosθ, y = a sinθ, k = 1 / ((Vb / Vr)² - 1), we have:

(x + k)² + y² = k² + k

The points defined by (x, y) satisfying above formula is a circle e with center P(-k, 0), and radius sqrt(k² + k).

Example code

import java.awt.geom.Point2D;

public final class EscapeCircle {
  public Point2D.Double center;
  public double radius;

  public EscapeCircle(Point2D.Double center, double radius) {
    this.center = center;
    this.radius = radius;
  }

  public static EscapeCircle calc(Point2D.Double fireLocation, Point2D.Double targetLocation, double waveSpeed) {
    double distance = fireLocation.distance(targetLocation);
    double k = 1. / (sq(waveSpeed / 8.) - 1.);
    double radius = distance * Math.sqrt(k * k + k);

    return new EscapeCircle(scale(fireLocation, targetLocation, 1 + k), radius);
  }

  private static Point2D.Double scale(Point2D.Double origin, Point2D.Double point, double ratio) {
    return new Point2D.Double(
        origin.x + ratio * (point.x - origin.x),
        origin.y + ratio * (point.y - origin.y)
    );
  }

  private static double sq(double x) {
    return x * x;
  }
}

See also

• Escape Envelope
• Maximum Escape Angle
• Shape of the escape envelope