Talk:kd-tree
Contents
Bucket PR k-d tree
I think you all know about Bucket PR k-d tree (aka Simonton's tree), right? I'll get directly to my point.
The Bucket PR k-d tree (I'll refer as just a tree from now on) is a binary tree split by the median of the bound, right? I wonder if I make it m-ary tree, let say, Ternary or Quaternary tree instead of just binary? Will it better? » Nat | Talk » 09:12, 15 August 2009 (UTC)
Note, it doesn't by definition have to be split by the median, though the median is usually considered the best place. As far as your second question... it may be better, or it may not. I'm pretty sure it will depend heavily on the implementation details and the data set in question. --Rednaxela 14:51, 15 August 2009 (UTC)
In a binary tree you do 1 comparison to narrow it down to 1/2 the tree (if it's well balanced). In a 3-ary you do (on average) 1.5 comparisons to narrow it to 1/3. 4-ary 2 comparisons for 1/4 of the tree. 1*1/2 = 1.5*1/3 = 2*1/4. They're all theoretically the same. --Simonton 15:33, 15 August 2009 (UTC)
- Also note that with a 4-ary tree it's best to do a binary search at each node, which is pretty much the same thing as going back to a binary tree, except you'd be doing two comparisons for the same dimension instead of stepping to the next. --Simonton 15:36, 15 August 2009 (UTC)
(Edit conflict) It could be faster splitting 4-ways, sure, but my gut says not by very much. I'd probably recommend doing the normal 2-way (binary) one first, since it will be much simpler to develop and to debug, and then you can try to modify it to do 4-way. You'll need the 2-way version, anyway, in order to compare the speeds. Good luck. --Voidious 15:38, 15 August 2009 (UTC)
It seems that Ternary tree is the fastest of binary, ternary and quaternary. But I've some question, does the Kd-Tree output the same as linear (brute-force) search. Some of my test state that:
Starting Bucket PR k-d tree performance test... Generating points... Data generated. Performing linear search... Linear search complete; time = 0.003425156 Performing binary k-d tree search... Binary tree search complete; time = 0.001995574 : accuracy = 0.4666666666666667 Performing ternary k-d tree search... Ternary tree search complete; time = 2.91098E-4 : accuracy = 1.0 Performing quaternary k-d tree search... Quaternary tree search complete; time = 3.22178E-4 : accuracy = 1.0
Data completely random. Accuracy calculate by number of result that is same as linear / cluster size. This test with a hundred data points and cluster size of 15. If I increase the data points to 26,000 then the accuracy drop to zero. Is this my tree problem or it is known problem with Kd-Tree? » Nat | Talk » 16:34, 15 August 2009 (UTC)
The kd-tree should definitely give the same results as a brute force search, so you must still have some bugs to work out. --Voidious 16:38, 15 August 2009 (UTC)
- Really? Simonton's one sometimes wrong too! » Nat | Talk » 11:28, 16 August 2009 (UTC)
- Well, more test with m-ary tree and Simonton's and it seems that my tree and Simonton's have the exact same output but my linear didn't. I'll try your, Rednaxela's and Chase-san's one before conclude. Expected some kd-tree benchmarks this night (ICT), afternoon (UTC) or morning (EST) » Nat | Talk » 11:56, 16 August 2009 (UTC)
- Really? I'd be extremely surprised if Simonton's kd-tree had a bug in it. Maybe it's your linear search that has a bug instead (or also)? But I can say with 100% certainty that a kd-tree nearest neighbors search should produce the exact same results as a brute force nearest neighbors search. --Voidious 15:01, 16 August 2009 (UTC)
Your tree is the only tree on this site (exclude Chase-san's tree because his one doesn't have k-nearest neighbour search) that is perfect, see this:
RESULT << k-nearest neighbours search with flat/linear searching >>
: Used time = 447.54298 x 10^{-3} seconds
: Average adding time = 1.374 x 10^{-6} seconds
: Last node adding time = 2.4440000000000004 x 10^{-6} seconds
: Accuracy = 100%
RESULT << k-nearest neighbours search with Rednaxela's k-d tree >>
: Used time = 1265.16806 x 10^{-3} seconds
: Average adding time = 33.005 x 10^{-6} seconds
: Last node adding time = 19.696 x 10^{-6} seconds
: Accuracy = 86%
RESULT << k-nearest neighbours search with Simonton's Bucket PR k-d tree >>
: Used time = 96.38627 x 10^{-3} seconds
: Average adding time = 3.039 x 10^{-6} seconds
: Last node adding time = 3.423 x 10^{-6} seconds
: Accuracy = 80%
RESULT << k-nearest neighbours search with Nat's Bucket PR k-d tree >>
: Used time = 117.65993 x 10^{-3} seconds
: Average adding time = 3.368 x 10^{-6} seconds
: Last node adding time = 3.282 x 10^{-6} seconds
: Accuracy = 80%
RESULT << k-nearest neighbours search with Voidious' Bucket PR k-d tree >>
: Used time = 90.04413000000001 x 10^{-3} seconds
: Average adding time = 4.639 x 10^{-6} seconds
: Last node adding time = 3.562 x 10^{-6} seconds
: Accuracy = 100%
Actually, mine and Simonton's got all answers corrected, too, but I have this code in the answer checker:
if (Math.abs(linearAnswer[0].getDistance() - currentAnswer[0].getDistance()) > 0.00001)
accuracy *= 0.8;So they decrease to 80%. Input data for above result is quite large, k = 150 with 400000 data points with 15 dimensions. Here is another result with k = 5, points = 1000 and 4 dimensions:
RESULT << k-nearest neighbours search with flat/linear searching >>
: Used time = 9.28114 x 10^{-3} seconds
: Average adding time = 3.738 x 10^{-6} seconds
: Last node adding time = 7.613 x 10^{-6} seconds
: Accuracy = 100%
RESULT << k-nearest neighbours search with Rednaxela's k-d tree >>
: Used time = 3.67735 x 10^{-3} seconds
: Average adding time = 22.053 x 10^{-6} seconds
: Last node adding time = 65.302 x 10^{-6} seconds
: Accuracy = 60%
RESULT << k-nearest neighbours search with Simonton's Bucket PR k-d tree >>
: Used time = 2.47867 x 10^{-3} seconds
: Average adding time = 8.007 x 10^{-6} seconds
: Last node adding time = 4.959 x 10^{-6} seconds
: Accuracy = 80%
RESULT << k-nearest neighbours search with Nat's Bucket PR k-d tree >>
: Used time = 3.32095 x 10^{-3} seconds
: Average adding time = 5.402 x 10^{-6} seconds
: Last node adding time = 5.238 x 10^{-6} seconds
: Accuracy = 80%
RESULT << k-nearest neighbours search with Voidious' Bucket PR k-d tree >>
: Used time = 0.21316000000000002 x 10^{-3} seconds
: Average adding time = 4.586 x 10^{-6} seconds
: Last node adding time = 3.5620000000000003 x 10^{-6} seconds
: Accuracy = 100%
Note [1]: This test suite was completely rewritten. The linear search is quite slow since I just basically Collections.sort() the points.
Note [2]: My tree is 6-ary tree with 22 buckets, which is the faster combination. The fastest isn't reveal yet that is why I create this test suite » Nat | Talk » 15:35, 16 August 2009 (UTC)
Hmm, interesting. I don't understand the part where you multiply by 0.8, even though you say they got all results correct. It looks like you're just comparing the distances on the first element - is it just because those two kd-trees don't sort the results before returning them? I also don't understand how my tree could have a total time of 1/10th of the others in that last test, though I wish it were true. =) --Voidious 15:49, 16 August 2009 (UTC)
Dunno why 0.8. But, when I change my answer checking code a bit, I accidentally remove Arrays.sort() so, yeah. They are 100% now, except Rednaxela's. About the time, yes it is true. And in first test it always stay there. Mine and Simonton's usually go between 60 and 300 × 10-3. Mine usually take more time, though. Note [3]: Data completely random. » Nat | Talk » 15:56, 16 August 2009 (UTC)
Oh, and I think that's why Diamond run faster than Dookious. Separate data from the tree seems to be a good idea, especially if you set your HashMap's density to 0.1 or something. » Nat | Talk » 16:01, 16 August 2009 (UTC)
Er.... this is strange. The test code I had showed my implementation having perfect accuracy... let me test again... --Rednaxela 16:16, 16 August 2009 (UTC)
- Ugh.... I found part of why your benchmark shows it so slow.... because of how you put:
public HyperPoint getPosition() {
return new HyperPoint(location);
}in the test code for mine... which would be a huge cause for slowness... --Rednaxela 16:33, 16 August 2009 (UTC)
After fixing that, and removing the weird 0.8 thing, I get results like:
RESULT << k-nearest neighbours search with flat/linear searching >>
: Used time = 19.19909 x 10^{-3} seconds
: Average adding time = 4.426 x 10^{-6} seconds
: Last node adding time = 8.032 x 10^{-6} seconds
: Accuracy = 100%
RESULT << k-nearest neighbours search with Rednaxela's k-d tree >>
: Used time = 4.16715 x 10^{-3} seconds
: Average adding time = 46.03 x 10^{-6} seconds
: Last node adding time = 9.987 x 10^{-6} seconds
: Accuracy = 100%
RESULT << k-nearest neighbours search with Simonton's Bucket PR k-d tree >>
: Used time = 14.88995 x 10^{-3} seconds
: Average adding time = 11.440000000000001 x 10^{-6} seconds
: Last node adding time = 9.289000000000001 x 10^{-6} seconds
: Accuracy = 100%
RESULT << k-nearest neighbours search with Nat's Bucket PR k-d tree >>
: Used time = 5.1635800000000005 x 10^{-3} seconds
: Average adding time = 38.910000000000004 x 10^{-6} seconds
: Last node adding time = 10.337000000000002 x 10^{-6} seconds
: Accuracy = 100%
RESULT << k-nearest neighbours search with Voidious' Bucket PR k-d tree >>
: Used time = 0.28069000000000005 x 10^{-3} seconds
: Average adding time = 9.144 x 10^{-6} seconds
: Last node adding time = 8.520000000000001 x 10^{-6} seconds
: Accuracy = 100%
most of the time, but if I re-run it, sometimes mine gets lower scores. I'll try and figure out what is happening with that. Haha, my adding speed really is terrible compared to my searching speed. --Rednaxela 16:43, 16 August 2009 (UTC)
Hmm.. alright... I'm now working on a new k-d tree that should be even more efficent than the Voidious one I believe... :) --Rednaxela 23:04, 16 August 2009 (UTC)
Curses... my attempt to make a better kd-tree by using heap-style storage of the tree has failed. While it would be efficent, the kd-tree is insufficently balanced and too sparse, causing the size of array that needed to be allocated to be HUGE :( --Rednaxela 03:30, 17 August 2009 (UTC)
- How much do you define HUGE? If it is ~200MB, it is acceptable, at least for me =) » Nat | Talk » 15:21, 17 August 2009 (UTC)
- Oh... as in... it causes Java to run out of memory with default settings, at just 4000 data points... that's what I mean by huge :) --Rednaxela 15:25, 17 August 2009 (UTC)
(Continue on User talk:Nat/k-d tree benchmark)
I have some thoughts that may be related to this, as it promises to be an interesting (ie. long) discussion, I think it should be on a different page : User:AW/Kd-Tree/thoughts --AW 01:00, 14 March 2011 (UTC)
Well, from some experiment with my slow m-ary k-d tree, I found that m-ary is slightly to much faster depends on number of dimension due the number of points to considered. But the slowest point of m-ary tree that make this kind of tree slower than binary k-d tree in most cases is the recursion part. Say 10-ary tree and the closest children to the center is the 6th child. Best way to do recursion is by the order 6,5,7,4,8,3,9,2,10,1. But the if/for that doing that is very expensive, it can be slower than my old, very-unoptimized linear search sometimes (6-ary with 22 bucket size, binary with 8 buckets would be up to 5 times slower). So until we can come up with better solution except hard-coded (switch(childIndex) case 1: order = new int[]{1,2,3,4,5,6,7,8,9,10} ... ), I'd say that binary is the best solution now. » Nat | Talk » 14:25, 28 August 2009 (UTC)
- Hm yeah... that aspect is tricky. As far a speed though, I'm really quite doubtful that a m-ary tree can be faster than plain binary tree, at least when the binary tree is highly optimized and is smart about dimensions to split on. I'm pretty sure the asymptotic bounds on time are the same, but the well-optimized binary tree requires considerably simpler logic (like you just give) to to determine the flow of the program. I have a hunch that the only reason it's faster for you in some circumstances, is due to needing to recurse fewer times to hit the same number of nodes. I could try hacking a 3-ary version of my efficient kd-tree up, but I strongly doubt it would do any better. --Rednaxela 14:44, 28 August 2009 (UTC)
Spelling
Hmm... How this spell? kd-tree or k-d tree? Wikipedia spell it as kd-tree. But the real name is k-dimensional tree so I think it should be k-d tree. » Nat | Talk » 02:10, 23 August 2009 (UTC)
- I'd say either "kd-tree" or "k-d tree" is okay. Google indicates that either is just as valid. Another note, is that if you capitalize it as in a title, it's "k-Dimensional Tree" with a lowercase k, therefore the shortened name would be either "k-D Tree" or "kD-Tree". This article should have the capitalization of 'k' and 'd' swapped :) --Rednaxela 03:35, 23 August 2009 (UTC)
- Actually... I'm not sure about the capitalization of the shortenings. I see "Kd-Tree", "kD-Tree", "KD-Tree" and "KD-tree" all used. I suspect... that nobody anywhere really knows :) --Rednaxela 03:41, 23 August 2009 (UTC)
Tree Iterator
From what I can tell, ABC, in Shadow, does a lot of unnecessary work in pulling clusters that are bigger than necessary so that some of the results can be eliminated by out of bounds checking of the Play It Forward algorithm. How about instead having a 'tree iterator' which is initialized with a point to find neighbors to, and progressively finds the next cluster point as .next() is called? It simply stores the state of the search between calls to .next() so that the search for the next point can be resumed the moment .next() is called again. --Skilgannon 10:44, 3 September 2009 (UTC)
Hmm... I think it isn't impossible but the tree will be far more complicated. Issue that may raise is about the left/right child. Say 2 dimensions, bucket size of 1: [0.49,0] [0.51,0] [0.51,1] ... and you request 2 neighbours with center of [0.51,0]. Say it split on 0.5, on the root it will cluster first point to the left child and other two in right child. The tree will recursive into right child first and add its 2 data points into the result heap/pq/list/whatever you want. Now when it recursive into left child it will find that the data on left child is closer to center than the third data which is on the right child of the root node. If the tree go very deep this can cause a lot problem with tree iterator... Hope you understand what I'm trying to point. » Nat | Talk » 11:50, 3 September 2009 (UTC)
That's certainly an interesting thought Skilgannon. It really wouldn't be that much more complicated, however I do fear that it would be less efficent really. All it would take is storing the results in a min-heap instead of a max-heap, always calculating the distance to the path not taken, and as soon as it gets to a leaf, checking if any path not taken could possibly have something closer. That does however force extra calculations. Doing that would require an ugly amount of code-duplication as well. I might make an alternative version of the tree that supports this but I'm not sure it's worth keeping in the main version... Unless... it's somehow so efficent that I might as well just call 'next' n times to get the nearest n neighbours, but I doubt it'll be that good no matter how well I optimize it. It might be worth a try though... --Rednaxela 13:00, 3 September 2009 (UTC)
Well... after giving it some more thought... I think I may just be able to implement it without measurable efficency loss... I'll give it a try when i get back home later today :) --Rednaxela 13:24, 3 September 2009 (UTC)
- That would be such a nice tree, what I like about this idea is that we wouldn't be forced to use a static cluster size, if the last processed point is close enough to the center we could keep pulling values. --zyx 15:21, 3 September 2009 (UTC)
Disputed claim
The recently added part "PR means the tree cycles through split dimensions in a constant order. This is faster to calculate than other strategies like splitting on the dimension with the largest variance." I would disagree with. In testing of my kd-tree, I've found that using the widest variance led to measurable performance gains compared to cycling through split dimensions. Now, part of why my implementation is fast with widest variance splitting may be that I track the bounding orthotope (bounding box). Even without that though, I don't see why cycling would be be more efficient unless the node size is huge since 1) It mostly affects insertion speed and insertion is generally about two orders of magnitude faster than searches and often needs to occur less frequently, and 2) There's almost no way the search could be slower with 'widest-variance' if branches remember their split dimension, unless the input data is particularly manipulative as to fool it. --Rednaxela 20:17, 25 February 2010 (UTC)
If you're disputing the description of the PR part, I got that from a Google Book result for one of the books written by the author of the linked to page (Hanan Samet, Foundations of multidimensional and metric data structures, p 71).
If you're disputing the speed part, the claim refers to the speed of calculating which dimension to split on. You can't beat (parent split dimension + 1) when it comes to speed. I presume what you refer to is speed of searching/adding. If that is your metric, splitting on the dimension with largest variance should often be faster as it gives you more meaningful splits, letting you ignore more points during a k-NN search. —duyn 02:19, 26 February 2010 (UTC)
Hey Duyn, in this context PR stands for Point-Region, not the way the tree cycles through its dimension splitting. Also, that sentence can be misleading. It is not clear that the 'faster to calculate' only refers to which dimension should be split next, and not the combined store/retrieve cycle. Not only this, but it seems to contradict the bullet point above it, which states that "we can choose a smarter splitting point than whatever we receive first", which is not only referring (I believe) to where in the splitting dimension the split should take place, but also what dimension the split should take place in. --Skilgannon 05:47, 26 February 2010 (UTC)
Thanks for clarifying that. That part wasn't in the Google Books Preview. I've updated the PR part to reflect what wikipedia describes as a region quadtree, which is what the demo applet on the linked page seems to do. I don't see how the Point part comes into it, though. —duyn 16:03, 26 February 2010 (UTC)
Performance Graph!
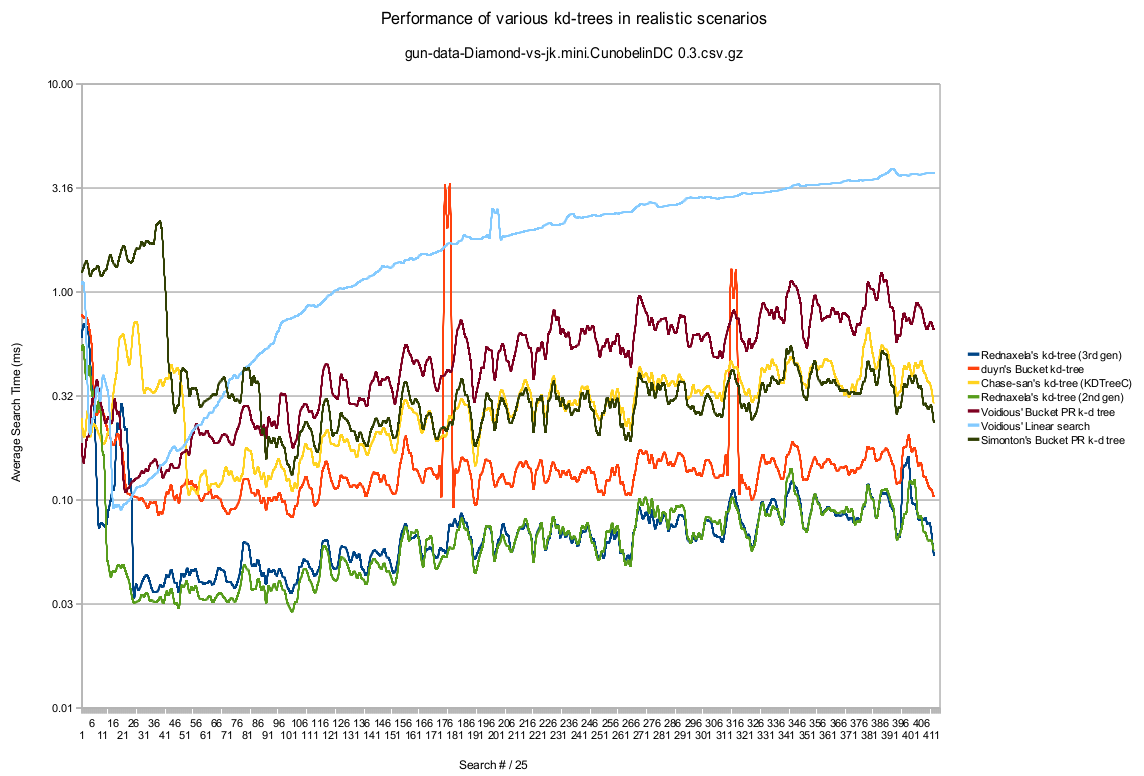
I was frustrated at how the benchmark tool's "average worst searching time" doesn't really characterize how the search times changes as the battle progresses, so I made the above graph. It's based on the real searches performed in a battle by Diamond, and only repeats for one iteration so the data is noisy, but I did so so the JIT-compiler's impact at the start of battle for each tree can be seen. Note, how fast the JIT-compiler kicks in is very non-deterministic, but this gives a general picture. So, what to people think of this graph? Any comments on the results? Think it should go anywhere? --Rednaxela 07:45, 5 March 2010 (UTC)
- Oh wow seeing the performance like this is very interesting. It also shows how the trees handle the congested period before the JIT starts working to full effect. Interesting to see duyns spike like that. Is he rebuilding/rebalancing the tree during those periods? MY algorithm seems about on par with Simonton's. Your 2nd generation tree actually seems to preform better at the start then your 3rd gen, but regardless, you still have the best one. I wonder what voidious is doing different in his. As for a place to put it, maybe make a statistics page? --Chase 08:08, 5 March 2010 (UTC)
- I don't track the bounds of the hypercube below any given node. I imagine that's one of the bigger factors. Maybe I'm wrong. I'd probably switch to Red's tree before improving mine much. :-P --Voidious 14:58, 5 March 2010 (UTC)
- Well, I didn't think Simonton's tracked bounds either. About the difference between my 2nd and 3rd generation ones at the start, that's what I meant by the JIT-compiler being non-deterministic, because I find that between my 2nd and 3rd generation, the difference at the start can lean in either direction. --Rednaxela 15:38, 5 March 2010 (UTC)
- Yeah, not sure what's the diff there, but the extra hypercube checks help a lot, right? Between me and Simonton it could even be bucket size or something minor. And Chase, feel free to change the ordering/description of the trees, I didn't put that there anyway. =) As much as seeing this graph tempts me to tinker with my kd-tree performance, I can't help but focus on stuff that will actually close the gap to DrussGT. =) --Voidious 17:50, 5 March 2010 (UTC)
- Wow, those are some really big spikes in my tree. I don't have dynamic rebuilding or rebalancing in my tree, so it would be an interesting adventure to track down the source of those spikes.—duyn 23:21, 5 March 2010 (UTC)
So here's what the graph looks like if one only cares about performance averaged over 100 repetitions, with and extra 5 repetitions at the start thrown out to remove the affect of the JIT compiling at the start.
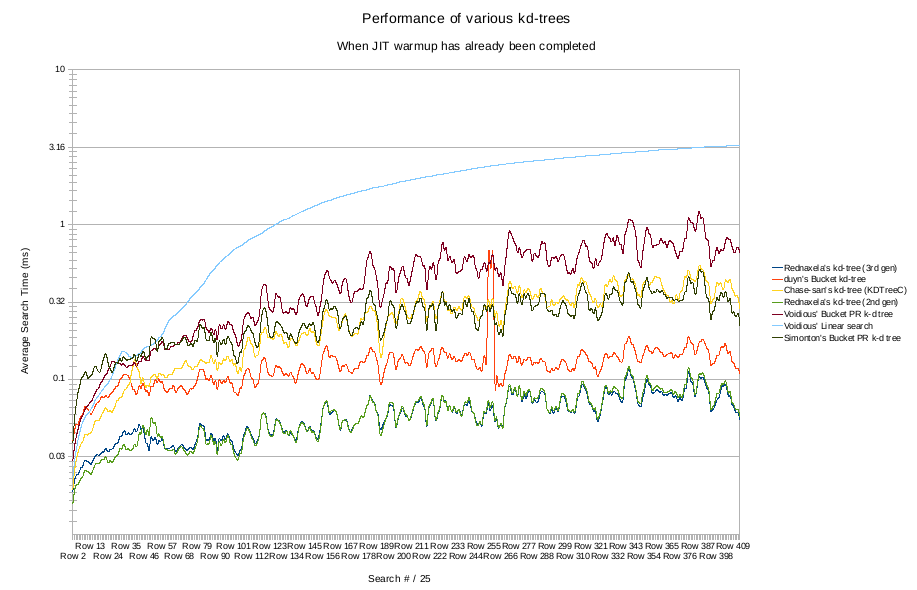
I find it interesting how clear 'easy' and 'hard' searches are here. Also, it's probably worth reminding that both of these graphs are on a log scale, not linear scale. That is in order to fit the linear search on the same graph as the rest. --Rednaxela 15:38, 5 March 2010 (UTC)
Updated chart with Duyn's tree updates, also comparing showing how normal scale and log scale:
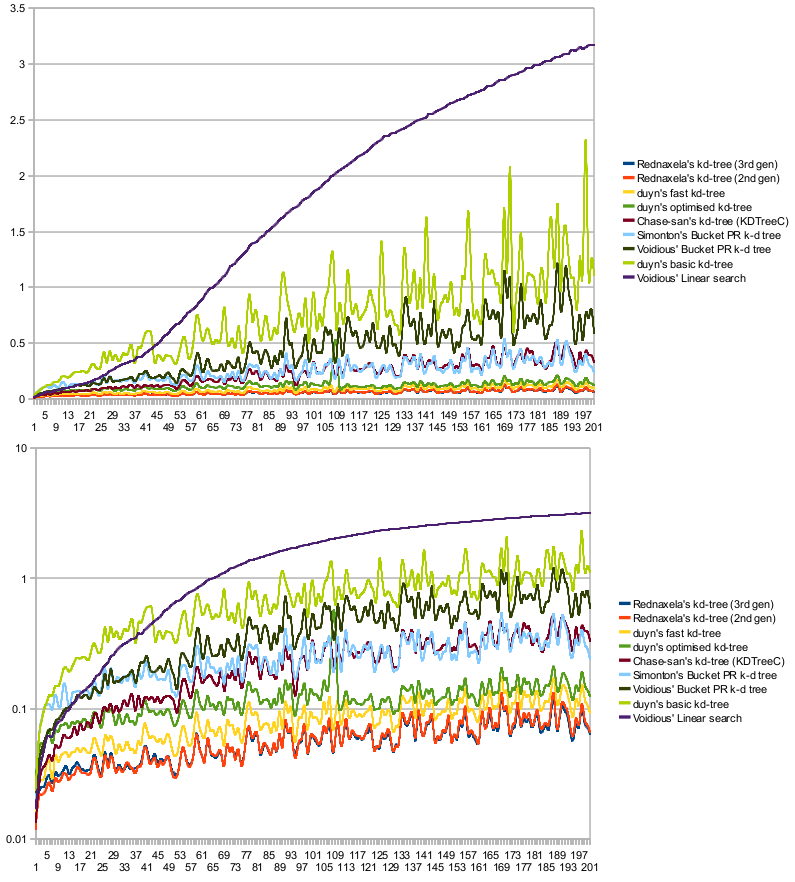
--Rednaxela 03:36, 13 March 2010 (UTC)
- Interesting how the spikes observed before only show up in my TreeMap-using variant. This suggests they were due to something TreeMap was doing.—duyn 06:06, 13 March 2010 (UTC)
- Looking at the non-log one, I no longer feel so bad about my trees performance. (Technically using the same first generation techniques as Simonton's, which is why they are so close, except my output is sorted). --Chase 11:06, 14 March 2010 (UTC)
So, I wanted to get a better idea how the JIT impacts results throughout the battle, so I modified the benchmark to run every test iteration and each tree in it's own separate JVM (using serialization to pass in the test data/parameters, and pass the results back). Here are the results of 100 iterations, with a fresh JVM for each test:
BEST RESULT: - #1 Rednaxela's kd-tree (3rd gen) [0.0704] - #2 Rednaxela's kd-tree (2nd gen) [0.0750] - #3 Rednaxela's kd-tree (3rd gen, iterated) [0.1045] - #4 duyn's fast kd-tree [0.1055] - #5 duyn's optimised kd-tree [0.1203] - #6 Chase-san's kd-tree (KDTreeC) [0.2489] - #7 Simonton's Bucket PR k-d tree [0.3950] - #8 Voidious' Bucket PR k-d tree [0.5337] - #9 duyn's basic kd-tree [0.8358] - #10 Voidious' Linear search [1.8134] Benchmark running time: 6762.90 seconds
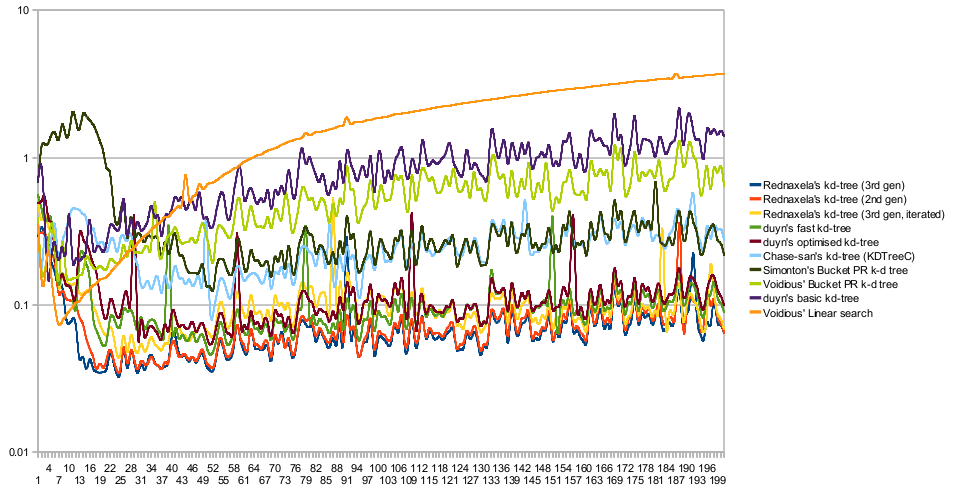
The linear search takes a clear lead at the very start since it's far simpler for the JIT compiler, but very quickly the others pull ahead :) --Rednaxela 00:27, 15 March 2010 (UTC)
These graphs look pretty noisy, but consistently noisy. I think it may be handy to remove Void's flat search from the data and graph against the average of all the trees. e.g. Red's 3rd generation line should be Red's 3rd generation value minus the average of all tree values for that horizontal position. This would remove interference from background processes and give you some smoother performance lines. --Martin 21:44, 15 March 2010 (UTC)
- Err... you just overwrote the new comment/graph I added above. Fixed now. Anyway, that noise isn't due to background processes Martin. That "noise" is because some searches are simply more difficult than others for the tree. Notice how Voidious's linear search has a smooth line, also notice how the peaks/dips are mostly the same for all of the trees. The only true 'noise' is of a magnitude visible in the linear search line, in other words, pretty negligible. If making it look flatter is desirable despite the bumps not being noise, I think a ratio would make more sense than subtracting the fastest one, due to how the peaks/dips become larger as the average becomes larger. --Rednaxela 22:09, 15 March 2010 (UTC)
Possible error
I am still learning about kD-Trees, but it seems to me that the following is incorrect: "For an applet demo, see Spatial Index Demos. The example there cycles partitioning axes in a fixed order, while most authors use a more intelligent algorithm. Rednaxela's kd-tree, for example, splits on the widest dimension." I have not looked at the code, but I think splitting on the widest dimension would always split along the same one, thus producing a very poor tree. Am I right? --AW 21:54, 12 April 2011 (UTC)
No, because the "widest dimension" depends on the data points in the bucket that is being split. For instance, if the 4 points in the node being split are (1, 0, 1), (1, 0.5, 1), (1, 0.75, 1), and (1, 0.8, 1), splitting on either the first or third dimension would do nothing, but the second (widest) dimension would give an even split somewhere between 0.5 and 0.75. It may be misleading to say "most trees" do this, actually, but Rednaxela and Duyn's do and probably any other new ones will too. --Voidious 21:59, 12 April 2011 (UTC)
Ok. When I read widest dimension I thought it referred to the bucket. ie. a bucket could be a rectangular prism and the longest side would be the widest dimension.--AW 22:38, 12 April 2011 (UTC)
- I think that is what it means, the widest side of the hypercube bounding the points in the bucket, but it won't be the same dimension every time because it will be examining a different set of points every time it splits. Depending on the distribution, splitting on the same dimension every time may even be the most balanced tree. Does that make sense? --Voidious 23:08, 12 April 2011 (UTC)
- That would be another way to phrase it, but the bucket and the hypercube bounding the points are not necessarily the same. So what it means is not "the widest dimension of the bucket." What it means is "the widest dimension of the hypercube bounding the points in the bucket." Which would, I think, be a clear way of stating it.--AW 23:21, 12 April 2011 (UTC)
Another thing, reading Rednaxela's quote above (the one in disputed claim), it sounds like the article used to say the "largest variance" instead of the "widest dimension." Does anyone else think that would be a more clear way of phrasing it?--AW 22:48, 12 April 2011 (UTC)
I think it means something like "Average value closest to center of dimension". For example there points (1, 1), (10, 2), (10, 3), (10, 4). If you will split by largest dimension, then result will be: (1, 1) in first node and (10, 2), (10, 3), (10, 4) in second node. But if you will split by largest variance, then result will be: (1, 1), (10, 2) in first node and (10, 3), (10, 4) in second node. I'm not sure, but i think, that variance can be calculated by some formula like this |(<min_dimension_value> + <max_dimension_value>) / 2 - <avg_values>| / |<max_dimension_value> - <min_dimension_value>| - distance between avg value and center of dimension, normalized by dimension width --Jdev 06:34, 13 April 2011 (UTC)
Okay... so two things here:
- AW is correct that "the widest dimension of the hypercube bounding the points in the bucket" is an accurate way of stating it. The distinction between the bounding hypercube and the bucket as defined by splits, is important.
- "variance" (in the fashion Jdev describes it) or "widest"? Both are valid approaches, but if I remember correctly I've found that "widest" is the most common adaptive approach taken in the papers I've seen about kd-trees. As a note, simply cycling through the axis is even more common in various papers, but it's less useful when you have data where he importance of any one axis is less certain, or more 'grainy'.
--Rednaxela 12:53, 13 April 2011 (UTC)
Just curious, did you every try splitting on median of the widest dimension? --Skilgannon 20:16, 8 October 2011 (UTC)
Help with my implementation that implements Collection
So, I've created an implementation that implements Collection (well extends AbstractCollection), but its performance in knn search is currently woefully inadequate. Using the knn-benchmark, I'm about a factor of 10 off. With that big a deficit, I'm probably make 1 (or more) glaring mistakes. I would really appreciate any feedback: https://bitbucket.org/lessonz/collections/overview and specifically: https://bitbucket.org/lessonz/collections/src/be153492f5aac72c8d2918efd1393a77fb808104/src/main/java/lessonz/collections/kdtree/bucketpr/BucketPRKDTree.java?at=default Thanks. --Lessonz
Sorry I didn't notice your post earlier. I don't have time to look in detail right now, but giving it a quick look, you're making some of the same mistakes that I made in my first attempt at a kd-tree. IIRC, use of the Comparator classes, and seperate classes for leaf and branch nodes also adds a notable performance penalty. Your use of a KDPoint point class to contain things also adds a significant penalties. Use of the list object in the bucket is also adding some notable penalty. In summary, it looks like the main problems are to do with too much OOP-ness used for entities which are too small. If this was in C++, the highly granular use of objects may not hurt as much because objects can directly contain other objects without pointers to dereference, but because this is in Java, every object reference must be a pointer, and every pointer derefernce carries a penalty. --Rednaxela (talk) 17:30, 17 July 2013 (UTC)
Thanks Rednaxela. I really appreciate your input, and I was afraid that was the case. =) --Lessonz
- [View source↑]
- [History↑]
Contents
| Thread title | Replies | Last modified |
|---|---|---|
| bucket size | 3 | 07:50, 8 October 2013 |
| Mini-Sized | 5 | 20:07, 17 July 2013 |
It's the maximum size of the leaf in the tree. Seriously, you're trying to run before you can walk. You need to brush up on your Java and comp-sci theory before you start messing around with Kd-Trees. If you want more info though, this describes some of the features in the tree pretty well [1]
No idea. Probably about the same. Why are you so interested in Kd-Trees?
I'm not sure, if you leave out the complicated stuff it loses its speed. Perhaps with the help of built-in structures like Java's PriorityQueue it might be possible. Impress us!
I'd say... possibly, but there's no reason to. An efficiently implemented linear search will waste much less of the limited codesize, and ought to be fast enough, espescially given that the number of search dimensions that make sense to put in a Minibot is small. The first nearest-n-neighbor search bots didn't use kd-trees and worked just fine.
On the other hand... if you're wanting to do it for it's own sake, it would be real neat to see just how small it could get! :)
I will be rather busy over the next fortnight, but after that I could give it a try.
Do you, Rednaxela, know of any efficient, low-codesize linear search algorithms with multiple choice?
I ran across this while doing my KD-Tree research
http://www.michaelpollmeier.com/selecting-top-k-items-from-a-list-efficiently-in-java-groovy/
It looks like once you calculate your distances to everything (two for loops) it's just about 4 lines of code.
The trick with the performance of linear search is what method you use to keep track of the "N closest points so far". The methods in that article have a problem, because they're storing every point in the list in the PriorityQueue, sorted list or whatever other structure. That is inefficient. It's far better to store the only "N closest points so far". You can do this using PriorityQueue by removing the highest distance point from the queue whenever the queue's length is greater than N.
The optimal solution for speed of a linear search is to use a bounded-size heap to store the "N closest points so far" because you waste the fewest operations on points which are not within the N closest. PriorityQueue is implemented using a heap like this, however PriorityQueue is inefficient in practice due to Comparator/Comparable OOP stuff.
Personally I'd probably try making the smallest custom implementation of a heap that I could. Alternatively, you could use use Collections.sort() or PriorityQueue, however that adds it's own codesize because you have to have some wrapper object around points which implements Comparable/Comparator, and I fear that wrapper may add more codesize than tiny specialized implementation of a heap would.