Difference between revisions of "Maximum Escape Angle"
(revised text from old RandomTargeting page into its own article) |
(The work done at Maximum Escape Angle/Precise Positional needs to be seen! No pages were linking to it yet.) |
||
| (16 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | When firing, the largest angle offset from zero (i.e., [[Head-On Targeting]]) that could possibly hit an enemy bot, given the [[Game Physics]] of [[Robocode]]. | + | When firing, the Maximum Escape Angle (MEA) is the largest angle offset from zero (i.e., [[Head-On Targeting]]) that could possibly hit an enemy bot, given the [[Robocode/Game Physics|Game Physics]] of [[Robocode]]. |
== Calculation == | == Calculation == | ||
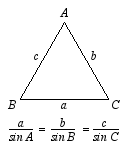
| − | Let's assume a triangle with sides <code>a</code>, <code>b</code> | + | Let's assume a triangle with sides <code>a</code>, <code>b</code> and <code>c</code> and angles (vertices) <code>A</code>, <code>B</code>, and <code>C</code>. <code>A</code> is the angle opposite to <code>a</code>, <code>B</code> is opposite to b, and <code>C</code> is opposite to <code>c</code>. The [http://en.wikipedia.org/wiki/Law_of_sines Law of sines] says that: |
| − | |||
| − | + | [[Image:LawOfSines.png|center]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Now let's say that your bot is in the vertex <code>A</code> and the enemy bot is in the vertex <code>C</code>. We will fire a bullet with angle <code>A</code> to hit the bot in vertex <code>B</code>. We know the value of <code>b</code> (it is the distance <code>D</code> from your bot to the enemy). | Now let's say that your bot is in the vertex <code>A</code> and the enemy bot is in the vertex <code>C</code>. We will fire a bullet with angle <code>A</code> to hit the bot in vertex <code>B</code>. We know the value of <code>b</code> (it is the distance <code>D</code> from your bot to the enemy). | ||
| Line 29: | Line 20: | ||
-> A = asin(Vr/Vb * sin(C)) | -> A = asin(Vr/Vb * sin(C)) | ||
</pre> | </pre> | ||
| − | We don't know the value of<code>C</code>, but we can take the worst scenario where | + | We don't know the value of <code>C</code>, but we can take the worst scenario where |
| − | <code>C = PI/2</code (<code>sin(C) = 1</code>) to get a | + | <code>C = PI/2</code> (<code>sin(C) = 1</code>) to get a Maximum Escape Angle of |
| − | <code>A = asin(Vr/Vb * 1 ) = asin (Vr/Vb)</code>. | + | <code>A = asin(Vr/Vb * 1) = asin (Vr/Vb)</code>. |
| − | With a maximum Robot velocity of 8.0, a theoretical | + | With a maximum Robot velocity of 8.0, a theoretical Maximum Escape Angle would be <code>asin(8.0/Vb)</code>. Note that the actual maximum depends on the enemy's current heading, speed, and [[Wall Distance]]. |
== See Also == | == See Also == | ||
| − | * [[ | + | * [[Maximum Escape Angle/Precise Positional]] - A more precise method of calculating Maximum Escape Angle, that doesn't require movement simulation. |
| + | * [[Maximum Escape Angle/Precise]] - A sophisticated calculation for Maximum Escape Angle, using [[Precise Prediction]]. | ||
| + | |||
| + | {{Targeting Navbox}} | ||
| + | [[Category:Robocode Theory]] | ||
| + | [[Category:Terminology]] | ||
Latest revision as of 13:39, 5 September 2012
When firing, the Maximum Escape Angle (MEA) is the largest angle offset from zero (i.e., Head-On Targeting) that could possibly hit an enemy bot, given the Game Physics of Robocode.
Calculation
Let's assume a triangle with sides a, b and c and angles (vertices) A, B, and C. A is the angle opposite to a, B is opposite to b, and C is opposite to c. The Law of sines says that:
Now let's say that your bot is in the vertex A and the enemy bot is in the vertex C. We will fire a bullet with angle A to hit the bot in vertex B. We know the value of b (it is the distance D from your bot to the enemy).
We don't know c, but we know that it will be the distance traveled by the bullet. Also, we know that a will be the distance traveled by the enemy bot. If we put a, b, and c as a function of time, we have:
b = D c = Vb * t (Vb is the bullet speed) a = Vr * t (Vr is the enemy bot velocity)
Now, using the Law of sines:
a/sin(A) = c/sin(C) -> Vr*t / sin(A) = Vb*t / sin(C) -> sin(A) = Vr/Vb * sin(C) -> A = asin(Vr/Vb * sin(C))
We don't know the value of C, but we can take the worst scenario where
C = PI/2 (sin(C) = 1) to get a Maximum Escape Angle of
A = asin(Vr/Vb * 1) = asin (Vr/Vb).
With a maximum Robot velocity of 8.0, a theoretical Maximum Escape Angle would be asin(8.0/Vb). Note that the actual maximum depends on the enemy's current heading, speed, and Wall Distance.
See Also
- Maximum Escape Angle/Precise Positional - A more precise method of calculating Maximum Escape Angle, that doesn't require movement simulation.
- Maximum Escape Angle/Precise - A sophisticated calculation for Maximum Escape Angle, using Precise Prediction.
| ||||||||||||||||||||||||||||||||||||