Difference between revisions of "Maximum Escape Angle/Precise Positional/Non-Iterative"

From Robowiki
Jump to navigation Jump to search
m (fix)
m (Update HighRes Illustration Graphics)
 
(3 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
[[File:EscapeCircle.png|600px]]
+
{{Stub}}
  
−
Consider a situation where a bullet fired from the firer A hits the target C at some future position B. A is the angle opposite to a, B is opposite to b, and C is opposite to c.  
+
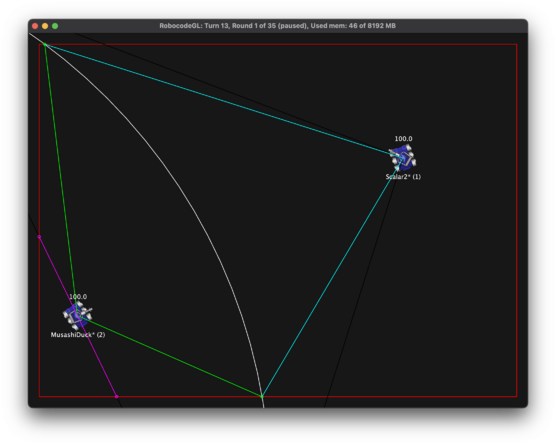
[[Image:Non-iterative PPMEA.png|frameless|Illustration of non-iterative PPMEA.|right|middle|556x445px]]
  
−
Let the target C be the origin, the distance and orientation from the target to the firer be the unit length and positive x-axis respectively.  
+
'''Non-iterative PPMEA''' is a mathematical definition of [[PPMEA]] along with an algorithm to calculate it.  
  
−
Let θ be the angle between b and a, we have c / a = Vb / Vr, b = 1, where Vb and Vr is the velocity of the bullet and the target respectively. Now consider cosine formula:
+
== Definition ==
  
−
a<sup>2</sup> + 1<sup>2</sup> - 2 a cosθ = (Vb / Vr a)<sup>2</sup>
+
Consider the [[Escape Envelope]] ignoring heading & velocity changing rules. Without walls, this area is essentially the area of [[Escape Circle]], in which PPMEA equals to traditional MEA. And with walls, it is the intersection of the area of the escape circle and the battle field (points reachable by a robot considering only walls).
  
−
Let x = a cosθ, y = a sinθ, k = 1 / ((Vb / Vr)<sup>2</sup> - 1), we have:
+
Then PPMEA can be defined as the angles between the line-of-sight and each of the pair of rays with maximum angle between them, where the rays are from firer to points in the [[Escape Envelope]] described above.
  
−
(x + k)<sup>2</sup> + 2 k x = 1<sup>2</sup> (k<sup>2</sup> + k)
+
== Algorithm ==
  
−
The points defined by (x, y) satisfying above formula is a circle e with center = P(-k, 0), and radius = sqrt(k<sup>2</sup> + k).  
+
The rays with the property described above can either by tangent rays to the circumference part of the outline of the escape envelope described above (in which PPMEA = Traditional MEA), or rays to the vertexes of the area (in which MEA is affected by walls).  
  
−
To find precise positional max escape angle, select the max of the escape angles calculated from the intersections of the above circle and the walls, or use traditional max escape angle when no intersection can be found.
+
With this in mind, to find PPMEA, take a collection of rays from firer to the intersections of the escape circle and the walls, along with the tangent rays to the escape circle whenever the intersection is within the battle field. The PPMEAs can be calculated by taking the maximums of the angles formed by one of the rays and line of sight, in either direction.
 +
 
 +
== See also ==
 +
* [[Escape Circle]]

Latest revision as of 13:30, 22 August 2021

This article is a stub. You can help RoboWiki by expanding it.
Illustration of non-iterative PPMEA.

Non-iterative PPMEA is a mathematical definition of PPMEA along with an algorithm to calculate it.

Definition

Consider the Escape Envelope ignoring heading & velocity changing rules. Without walls, this area is essentially the area of Escape Circle, in which PPMEA equals to traditional MEA. And with walls, it is the intersection of the area of the escape circle and the battle field (points reachable by a robot considering only walls).

Then PPMEA can be defined as the angles between the line-of-sight and each of the pair of rays with maximum angle between them, where the rays are from firer to points in the Escape Envelope described above.

Algorithm

The rays with the property described above can either by tangent rays to the circumference part of the outline of the escape envelope described above (in which PPMEA = Traditional MEA), or rays to the vertexes of the area (in which MEA is affected by walls).

With this in mind, to find PPMEA, take a collection of rays from firer to the intersections of the escape circle and the walls, along with the tangent rays to the escape circle whenever the intersection is within the battle field. The PPMEAs can be calculated by taking the maximums of the angles formed by one of the rays and line of sight, in either direction.

See also

Retrieved from "http://robowiki.net/w/index.php?title=Maximum_Escape_Angle/Precise_Positional/Non-Iterative&oldid=56982"