Reason behind using Manhattan distance
I have 2 hypotheses:
- Manhattan distance is more tolerant to noise than Euclidean distance. Squaring a dimension amplifies noise.
- Curse of dimensionality. Euclidean distance behaves oddly at high dimensions.
Squaring does not affect the order of nearest points, then with knn the same data points should be chosen.
And about noice
euclidean seems to be even more tolerant when noice has less energy than the main dimensions.
So manhattan seems to be more "elite-oriented", dropping points with offsets in another dimension more aggressively.
Anyway, according to https://datascience.stackexchange.com/questions/20075/when-would-one-use-manhattan-distance-as-opposite-to-euclidean-distance
Manhattan distance (L1 norm) may be preferable to Euclidean distance (L2 norm) for the case of high dimensional data:
Suppose there are 3 data points:
1 reference data point:
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
And 2 data points in the database:
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] (Euclidean distance = 3.87, Squared Euclidean distance = 15, Manhattan distance = 15)
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4] (Euclidean distance = 4, Squared Euclidean distance = 16, Manhattan distance = 4)
If noise changes a single 0 into a 4, it will affect Euclidean distance 4x times higher than Manhattan distance. Euclidean distance will pick the first, Manhattan distance will pick the second.
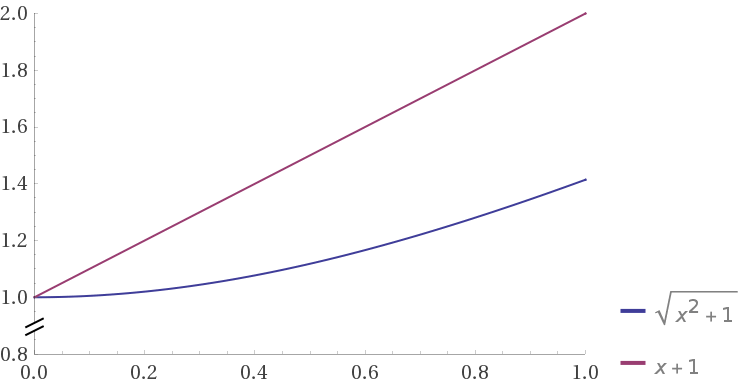
Shouldn´t you be adding that +1 to the x value before squaring?
Euclidean distance = sqrt( (x+1)^2 )
Manhattan distance = | x+1 |
my case is noise in another dimension ;)
however if noise is added to the main dimension,
it will be
sqrt((1 + x)^2 + 1)
vs
|1 + x | + 1
and if we put two curves together (shifted so that tey intersects on x=0)
http://robowiki.net/w/images/5/5a/C3BD3E15-EEB6-4F63-826F-7C1F5E54A78E.gif
euclidean looks terrible with large noise in one dimension, and manhattan looks robust.
I think it is due to the noise rejection. For me it is the ratio between how a small change in a lot of dimensions is weighted compared to a big change in a single dimension, as you demonstrated above. You can also think about it like the difference between L1 and L2 distance, how they would affect a minimization problem. L1 rejects large noises, and is the most robust you can get while still maintaining a convex search space. L2 has a gradient that gets larger the bigger the distance, so dimensions with more error are effectively weighted higher, and weighted higher than just proportional to the amount of error.